1.10　コンダクタンス

今回はコンダクタンスよ。コンダクタンスっていうのは、抵抗の逆数のことで、単位はジーメンス(S)。式で書くと、

G = 1 / R

よ。記号にはGを使うわ。 R₁ とか R₂ の代わりに G₁ とか G₂ って感じでね。次元も [ 1 / Ω ]で、つまりは [ A / V ]。抵抗とコンダクタンスの関係は、抵抗率と導電率の関係みたいなものよ。語源の conduct には「伝導する」っていう意味もあるの。ジーメンスは人命由来だけどね。

　なんでこんなパラメータを考えるかっていうと、前回で丸投げした並列回路の計算を簡素化するためよ。という訳でさっきの図、もっかい出すわね。

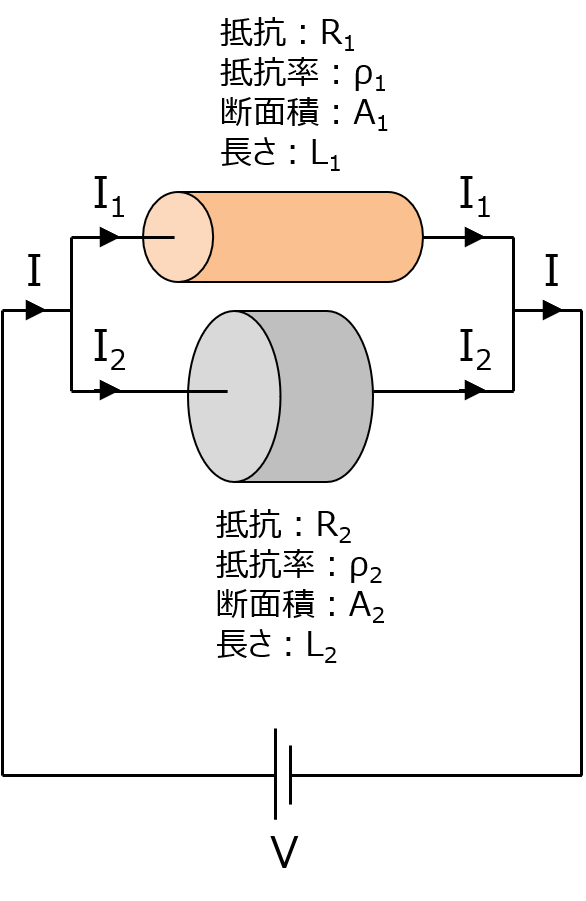
まず普通に、このまま全体の抵抗を考えるわ。図を見て分かる式を並べると、

I = I₁ + I₂
I₁ = V / R₁
I₂ = V / R₂

ね。という訳で全てを1つにまとめると、

I = I₁ + I₂
= V / R₁ + V / R₂
 = V ( 1 / R₁ + 1 / R₂ )

になるから、全体の抵抗 R(=V/I) は、

R = V / I

 = 1 / ( 1 / R₁ + 1 / R₂ )

になる。R₁ の逆数と R₂ の逆数を足して、さらに逆数にする。めんどくさいっしょ。だからここでコンダクタンスの概念を使えば、

R = 1 / ( G₁ + G₂ )

ってできる。ついでに言うと全体のコンダクタンスを考えることもできて、それは全体の抵抗の逆数だから、

1 / G = 1 / ( G₁ + G₂ )

ってなって、

G = G₁ + G₂

になるわ。これは並列になってる抵抗が3つとか4つになってても同じことで、とにかく全部足せば全体のコンダクタンスになるわ。これは、とある棒のコンダクタンスが

G = σ · A / L

になってて、並列っていうのは等価的に面積が増えるだけだからよ。

　でも実態として、わざわざコンダクタンスに変換せずに抵抗のまま計算することが多いわ。慣れてないと無理に活用して余計にチンプンカンプンになっちゃうことも少なくないし。そんな訳で、典型パターンをいくつかやってみるわよ。まず、抵抗が2つ。

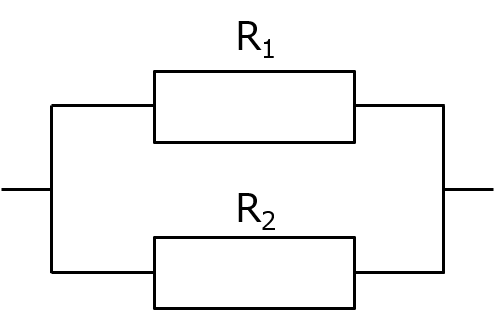
　これは上にも書いた通り、

R = 1 / ( 1 / R1 + 1 / R2 )

だから、ちょっと整理すると、

R = 1 / ( 1 / R₁ + 1 / R₂ )
= 1 / ( (R₂+R₁) / (R₁·R₂) )
= R₁ · R₂ / ( R₁ + R₂ )

になる。「和ぶんの積」とか言われるやつね。R₁ と R₂ の積を、和で割ってあげればいい。この中でも特に、R₂ が R₁ の n倍の値だった時。

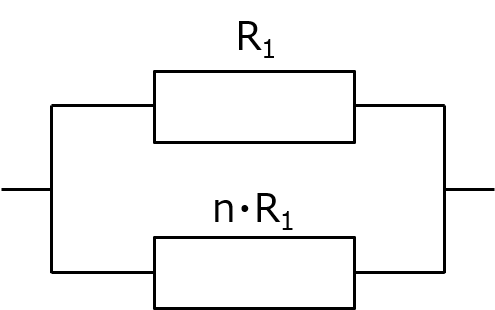
　この時は、

R = R1 · ( n·R₁ ) / ( R₁ + n·R₁ ) = n · R₁² / ( (1+n)R₁ ) = R₁ · n / ( n + 1 )

になるわ。並列は等価的に面積が増えてるだけって話だけど、抵抗が n倍 のものが継ぎ足された時っていうのは、面積が 1/n倍 のものが継ぎ足されたことになるから、

R = R₁ / ( 1 + 1 / n ) = R₁ / ( (n+1)/n ) = R₁ · n / ( n + 1 )

になるわ。

　次、3つ以上！

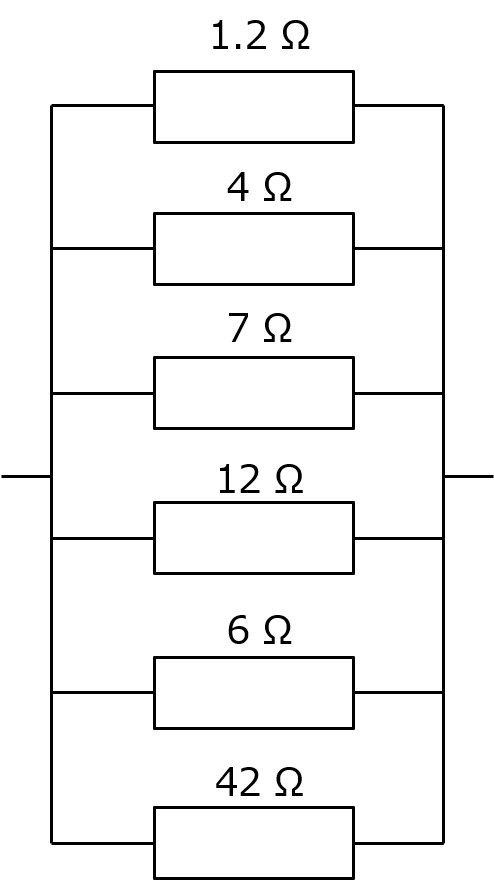
　うげーって感じね。全部が同じ抵抗値なら個数で割ってあげれば終わりなんだけど、世の中そんなに甘くないわ。
　もちろん、全部の逆数の和の逆数をとれば終わり。だけどまあ、ちょっと付き合って。抵抗が6個並んでるけど、同じ線で繋がれてる場所は全部同じ電位だから、入れ替えることもできるし、配線の分岐の仕方も変えられる。こうよ。

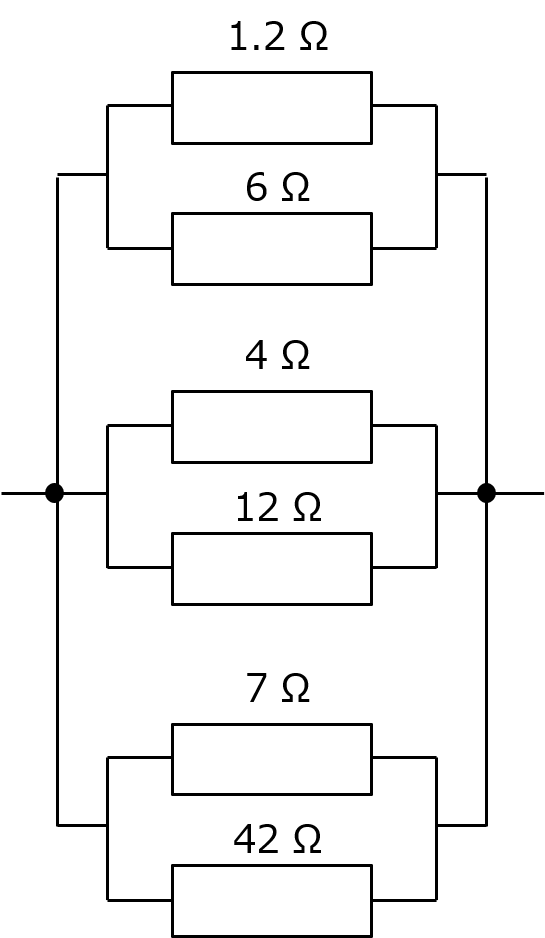
　分け方のコツとしては、とある抵抗とそのn倍の抵抗をペアにした時に、基になってる抵抗の抵抗値が n+1 の整数倍であることよ。そうすれば、n/(n+1)倍する時に、分母の n+1 が消えるから分数にならずに済む。4と12のペア、7と42のペアがそうなるわね。計算してみると、前者はnが3で、後者はnが6だから、

4 × 3 / ( 3 + 1 ) = 3
7 × 6 / ( 6 + 1 ) = 6

になるわ。もちろん「和ぶんの積」を使っても同じ数字になるからね。
　それから、1.2と6のペア。これは実は、6と30のペアを1/5したものだから、計算すると 1Ω になる。慣れてくると、1.2と6のペアを見た瞬間に「これは 1Ω になる」って分かるようになるわ。あとさりげなく図で十字の交差点には黒丸をつけてるけど、これは必須よ。T字はそのままでもいいけど十字はつけるのが鉄則。忘れないでね。

　という訳で、それぞれのペアで合成抵抗を出したからこうよ。

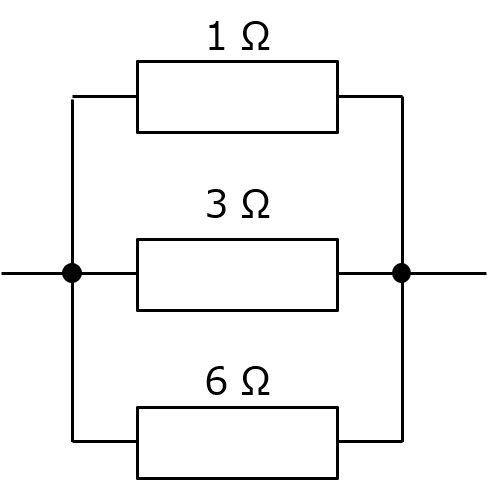
　ちょっとスッキリしたわね。簡単な数字だしこのまま逆数をとって計算してもいいんだけど、3と6のペアは 2Ω になるわ (こっちは定番だから計算抜きで脳内で済ませられるといいわね)。

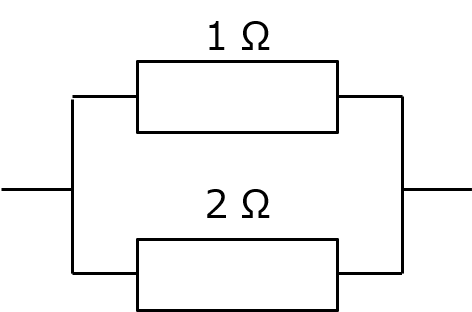
　あとは簡単ね。1Ω と 2Ω の並列で計算して、0.667Ω。テストの問題とかだと図があるだろうから、やるならこうかしら。

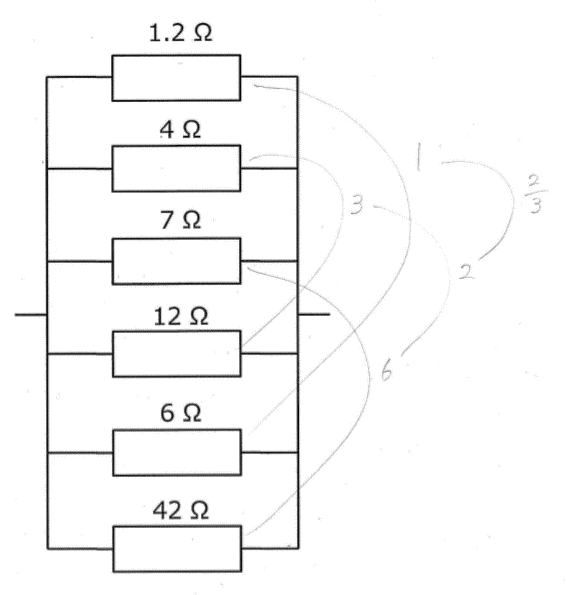
　という訳で面倒くさい分数の計算ナシで合成抵抗が求められたけど、この方法は、パッと見て分かった時だけ使うようにした方がいいわ。ペアの組み合わせ考えるのに時間使ってちゃ意味ないからね。関数電卓があれば一発で逆数とれるからチョチョイのチョイだし。でも関数電卓が禁止されてる資格試験もあったりするから気を付けてね。特訓しておくに越したことはないわよ。
　それから、こういうのは出題者の癖が強く出るもので、最終的な答えをスッキリさせるのが好きな人もいれば、そうじゃない人もいる。そうじゃない人が相手だと、ちゃんと逆数かコンダクタンスを使って計算しなきゃいけなくなるから、そっちのやり方も忘れないでね。