さぁ今度は抵抗よ。ここは電気講座だから単純に「抵抗」と呼ぶことにするけど、厳密には「電気抵抗」ね。単位はみんな大好きオーム(Ω)。やっと抵抗の話になるんだけど、導電率と抵抗率のページでほとんど話しちゃったね。てへ☆ぺろ。
とりあえず、オームの法則をもう1回かくわね。
I = V / R
V の代わりに E を使うこともあるけど、この講座では E は電界強度のことだから、電圧は V にするわ。オームの法則は他にも R = V / I だとか V = R· Iだとかあるけど、普通は電圧と抵抗が先にあって結果として電流が流れるから、私は I = V / R を基準にしてるわ。テストの問題とかだと「何アンペア流れてる」って与えられることも多いけどね。
実用上でも、「これの抵抗は何オームだろ?」って時は、何ボルトって決めて電圧をかけて、電流計で電流を測ってから抵抗を求めることがあるわね。理論的には材料とサイズとか形が決まれば計算できるけど、実際は理論とはズレるし、複雑な形になったら計算できない。
それじゃあ抵抗の計算の話に入るけど、棒1本での抵抗の計算は導電率と抵抗率のページでやっちゃったから数を増やすわね。まずは、こう。

直列接続ね。どっちも全く面積と長さで、材料も同じとするわよ。結論から言うと直列は足し算で、そう覚えてる人も多いと思うけど、なぜ直列は足し算なのかというと、
R = ρ· L / A
が基になってるのよ。全く同じものを2つ並べたから、単純にLが2倍になったのと同じ。間になんか線が入ってるけど、あれは普通は銅配線で、抵抗に使う材料に比べると抵抗率がかなりちっちゃいから無視することができるの。
じゃあ、太さも抵抗率も違うやつが並んだら? これも足し算すれば済む話なんだけど、ちょっと細かく見ていくわね。
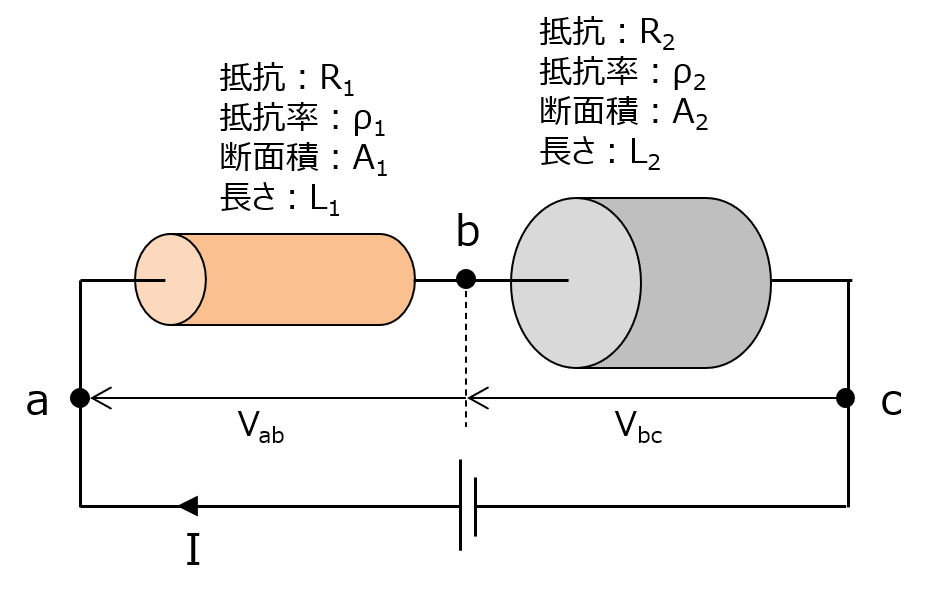
まず電流だけど、これはどの場所でも変わらない。電子が勝手に空気中に逃げ出すことはないから、ずっとこの回路の中をぐるぐると回ってるわ。次に電圧だけど、これは Vab と Vbc に分散される。しかも、
Vab + Vbc = V
になるわ。c点からa点への経路を考えた時に、電源を経由しても抵抗を経由しても2点間の電位の差は同じだからよ。詳しくは電圧のページを読んでね。
そしてこの回路全体の抵抗を考えるけど、これは
R = V / I
になる。オームの法則よね。全体の電圧を、全体の電流で割れば全体の抵抗になる。それじゃあ、「抵抗の直列接続は足し算」っていうのを知らない前提で進めて行くわよ?
まず、左側の抵抗を考えましょうか。まず真っ先に分かってるのは、
R1 = Vab / I
っていうのと、
R1 = ρ1 · L1 / A1
ね。ということは、
Vab / I = ρ1 · L1 / A1
が成り立つわよ。最終的に Vab + Vbc = V っていうのを使おうと思ってるから、左辺を Vab だけにするわね。するとこう。
Vab = I · ρ1 · L1 / A1
これと同じようにして右側の抵抗も考えると、Vbcは
Vbc = I · ρ2 · L2 / A2
になるわ。じゃあこれを Vab + Vbc = V に代入するわね。左右ひっくり返しちゃうけど、
V = Vab + Vbc
= ( I · ρ1 · L1 / A1 ) + ( I · ρ2 · L2 / A2 )
= I · ( ρ1 · L1 / A1 + ρ2 · L2 / A2 )
そして、全体の抵抗は V / I なのだから、I を左辺に持って行くと、
V / I = ( ρ1 · L1 / A1 + ρ2 · L2 / A2 )
= R1 + R2
完成! ちゃんと、「全体の抵抗 = 直列接続された2つの抵抗の足し算」になったわね。
次は並列について考えるわよ? まずは、同じものが2つ並んだ時。これも結論から言うと、全体の抵抗は半分になるわ。これも
R = ρ · L / A
を基に説明すると、全く同じものを2つ並列に繋いだら、面積が2倍になったのと同じになるから。
それじゃあ、違うやつが並列で並んだら? これについては、細かい計算は次のページに回すことになるけど、1つだけ確かなことは、「全体の抵抗値は、繋がれてるどの抵抗の抵抗値よりも小さくなる」ってこと。式で書くならば、
R < R1
R < R2
の両方が確実ってことよ。図で見るわね。
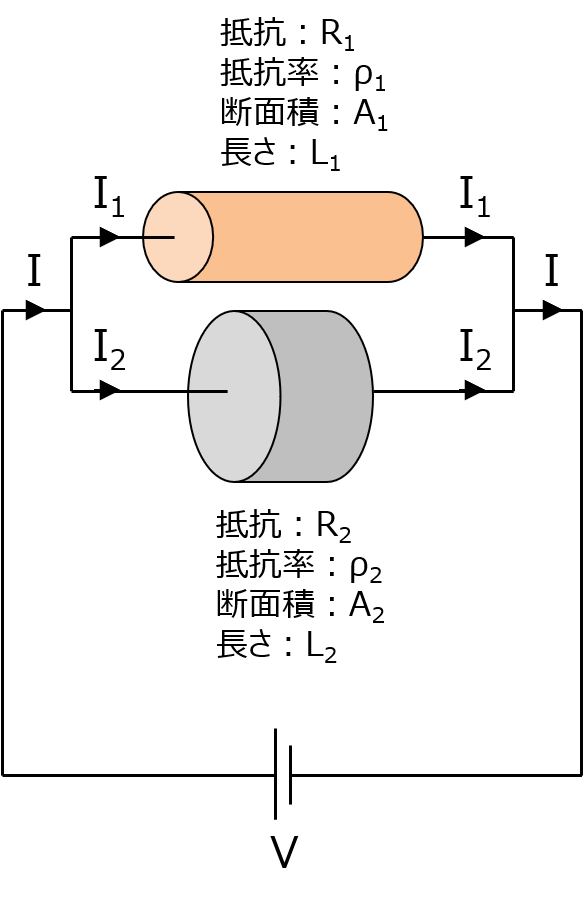
まず、I1 と I2 をそれぞれ計算すると、
I1 = V / R1
I2 = V / R2
よ。並列だと全部に同じ電圧がかかるわ。これが分からない人は電圧のページを読み直してね。で、全体の電流は
I = I1 + I2
になる。だって、電荷は空気中に逃げることはできないから、金属の道が2つに分かれても合計の電流は変わらないし、合流するときももちろん逃げずに全部戻る。ちなみにこれがキルヒホッフの第1法則よ。
話を抵抗に戻すけど、そもそも抵抗が R1 単体の時の電流は V / R1 で、R2 単体の電流は V / R2 なの。これに対して、並列に繋いだ時の電流はさっきも書いた通り
I = I1 + I2
だから、全体の電流は I1 よりも I2 よりも大きくなる。「全体の電流が抵抗単体の時の電流よりも必ず大きくなる」ということは、「全体の抵抗値は繋がれてるどの抵抗の抵抗値よりも必ず小さくなる」ということと同じよ。式の続きを書くと、こう。
I = I1 + I2
= V / R1 + V / R2
= V · (1 / R1 + 1 / R2)
なんとなく、「全体の抵抗値は繋がれてるどの抵抗の抵抗値よりも必ず小さくなる」って直感的に分かるわよね。1/Rn が足されるたびに電流が大きくなるんだから、全体の抵抗はどんどん小さくなっていくし、R1単体よりもR2単体よりも絶対に小さい。
さらにそもそもの話をするけど、電気回路の中での抵抗は、抵抗値さえ変えないようにすれば等価的に抵抗率とか他のやつも変えて考えることができるのよ。こんな感じ。
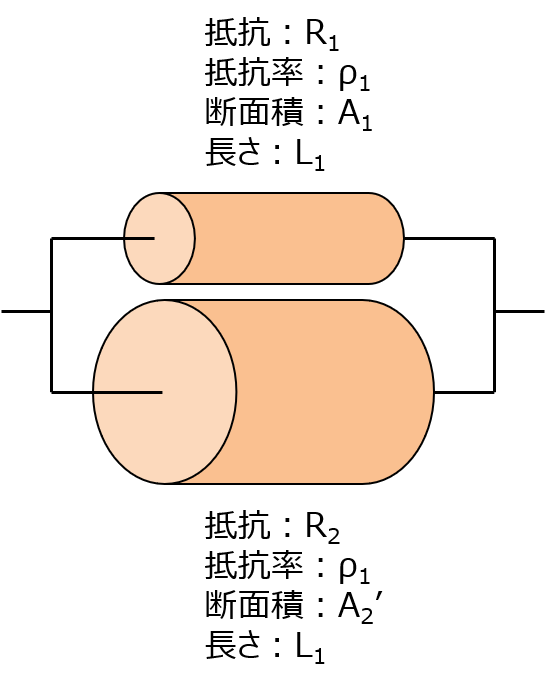
R2 の抵抗さんは、R2 の抵抗値はそのままに、抵抗率はR1さんと同じ ρ1 に、長さもR1さんと同じ L1 に、そして面積は、R2 の抵抗値が変わらないように調整されて A2’(エーツーダッシュ) になりました。
普通の回路計算だと「何オーム」って与えられて終わりで、抵抗率とかは載ってないでしょ? だからそれを利用させてもらって、抵抗率と長さは一緒って考えることにする。すると単純に、
R = ρ· L / A
のうちの A(面積) だけが増えてるってことになるわね。だから並列っていうのは、等価的に面積がどれくらい増えましたかっていうことでしかないのよ。それでも数値計算しようとすると面倒だから次のページでね。
ちなみに、直列についても、等価的に長さが増えただけって考えることができるわ。どのみち足し算だから単純だけど。
あと最後、抵抗で注意しなきゃいけないのは、同じモノを使っても、どこからどこまでの間の抵抗かでその値が変わることよ。例えば、球体の抵抗体があったとするわね。頑張ってこれに配線するとして、もう1本の線を反対側から取るか、2本ともすぐ近くで取るかで抵抗値は変わるわ。後者の方が抵抗体を通る距離が短くなるから、当然よね。
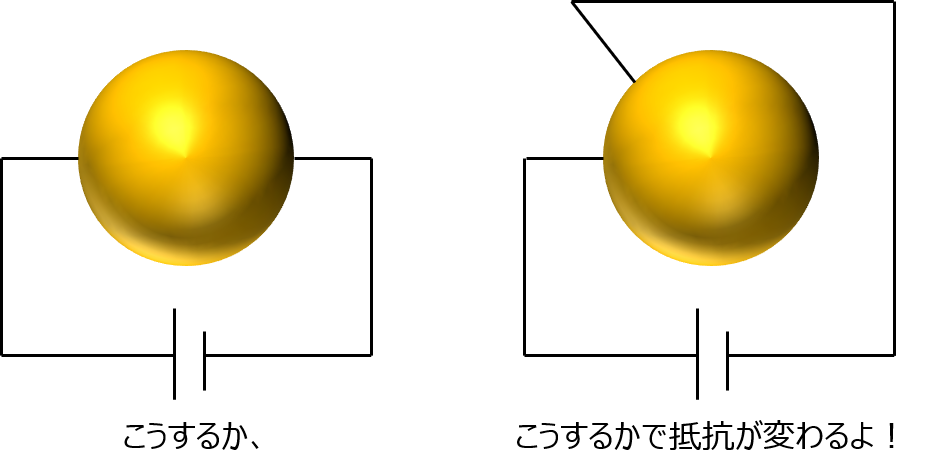
~column~
せっかくだから、並列とか直列とかじゃなくて、いびつな形のモノの抵抗はどうなるの? っていうのを考えるわよ。これでどう? プリンみたいな形してる棒。

考え方としては、直列と似たような考え方をするわ。これ、1つの巨大なプリンだけど、2つに分裂させることもできるわよ。
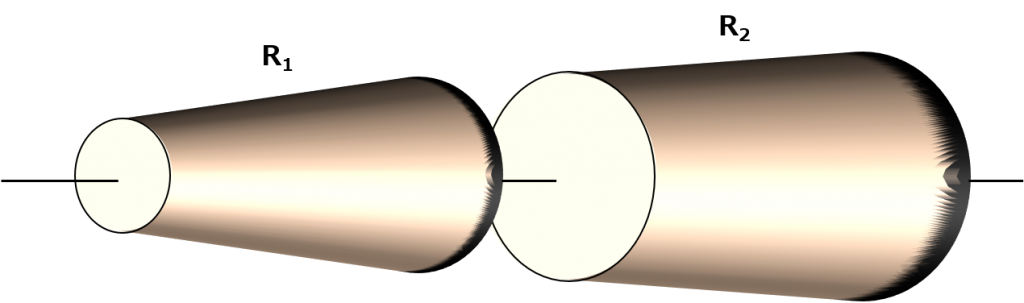
これで左のやつの抵抗と右のやつの抵抗を足せば合計の抵抗になるわ。って、いやいや、どっちもプリンじゃん! じゃあもっと分裂させてみましょうか。次は9個!

これで R1 から R9 までを全部足せばいいわよ。え? まだ1個1個がプリンに見える? しょうがないなぁ。これならどう?
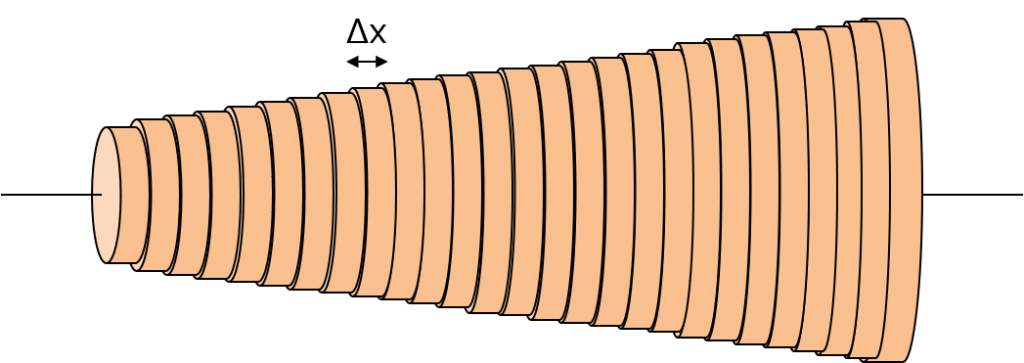
もはや何分割か数えるのも面倒くさいわね。絵の立体感が消えたのは気にしないで。とにかくちょー細かく刻んだから、1個1個は円柱よ。Δx はそれぞれの円柱の厚みのことね。
1個1個を円柱として扱えるから、それぞれの抵抗が計算できるわよ。ただし、注意しなきゃいけないのは、面積が場所によって違うこと。円の面積っていうのは半径で決まるから、こう考えましょうか。
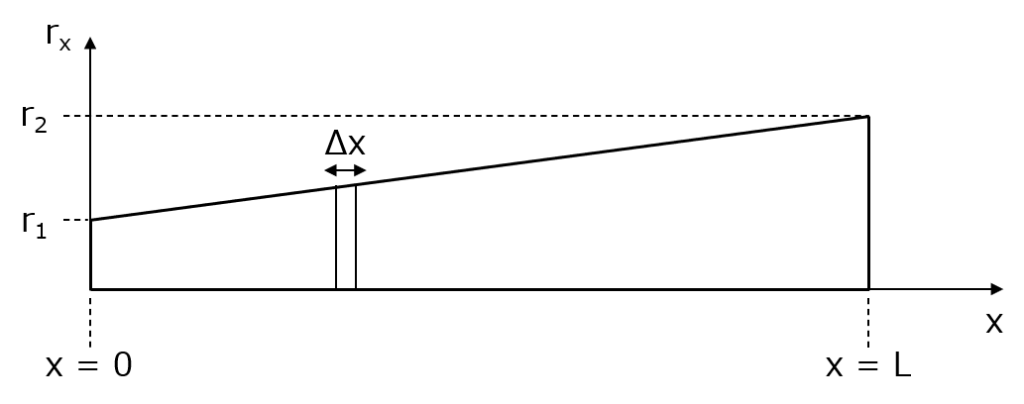
まず、x が変わると半径も変わるから、任意の x の場所の半径を rx とするわね。で、r1 と r2 の間の部分の半径はプリンの傾斜によって決まる。数学の話になっちゃうけど、傾斜を a とすると、
a = ( r2 – r1 ) / L
になるわ。だから、任意の x での半径 rx は、
rx = ( r2 – r1 ) / L · x + r1
になる。それで、任意の x での面積 Ax は、
Ax = π · rx2 = π· ( ( r2 – r1 ) / L · x + r1 )2
よ。π は円周率ね。カッコの展開をしてないけど、後でこのまま使うからいいのよ。とにかく、これでやっと任意の x の場所のスライスプリンの抵抗が計算できるわね。こうよ。
Rx = ρ · Δx / Ax
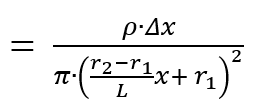
それで、このウジャウジャいるスライスプリンの抵抗を全部足せば全体の抵抗になるけど、何枚スライスなのかが分からない。そもそも Δx の数字さえ与えられてない。てか Δx は自分で作ったパラメータだ。
こんな時、どうするか。コラムを読むようなハイレベルの人は気付いてるかしら? そう、みんな大好き積分よ。え、好きじゃない? でもやんなきゃいけないからね。このプリン全体の抵抗は、こうよ。
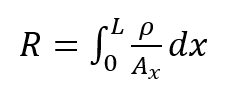
Δx が積分の ∫dx に化けました。そして積分範囲は x = 0 から x = L まで。つまり、こうなる。
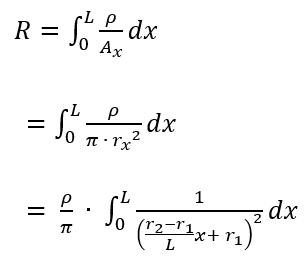
うわー。分母にx2乗の式がいっちゃったよ。でもしょうがないね。後半の積分の部分は、1 / ( ax + b )2 の不定積分は (– 1 / a) · 1 / ( ax + b ) + C になるから、
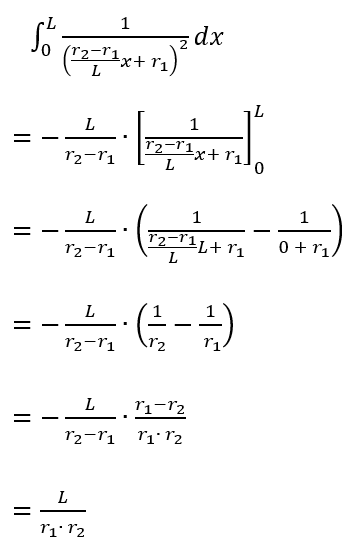
になるわ。これで R を計算すると、
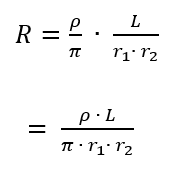
で終わり。いや~メンドくさかったわね~。積分を使うってなっただけでグッとレベルが上がるけど、抵抗の計算に限らず、積分の概念っていうのはここに書いた通りよ。細かく刻んで、任意の x の地点のパラメータ(今回は半径と面積)を考える。それで Δx を ∫dx に変えて、実際に積分計算をする。難しいけど、できるようになったら物理に強くなるから、頑張ってね。