1.8　抵抗率

　導電率の次は抵抗率よ。これは電流の流れにくさを示すもので、その値は導電率の逆数よ。つまり、

ρ = 1 / σ

ね。ρ は「ロー」って読むわ。導電率が材料ごとに決まってるから、抵抗率も材料ごとに決まってる。銅だと導電率が 5900万 S/m だったからその逆数で、1.69 × 10^-8 Ω·mよ。単位はそのまま「オームメートル」って読むわ。
　「毎メートル」ならともかく「かけるメートル」って何だよって思う人もいるかも知れないけど、次元を合わせるためにはこうなっちゃうの。前のページで、棒状の物体の抵抗値は

R = L / (σ· A)

になるって書いたわよね。σ = 1 / ρ だから、ρ を使って書くと

R = ρ· L / A

になるわ。見たことある人も多いわよね。抵抗率の単位は オーム・メートル(Ω·m) になってるけど、正確には、オーム・平方メートル・毎メートル(Ω · m² / m) よ。まず簡単な「毎メートル」から説明すると、とある太さの棒の、1メートル当たりの抵抗って意味よ。棒が長くなると電界が弱くなるから、棒としての抵抗値は大きくなるの。

　次、「オーム・平方メートル」だけど、面積が広いと一度に多くの電子が通れる(つまり電流が大きくなる)から、棒としての抵抗は小さくなるの。
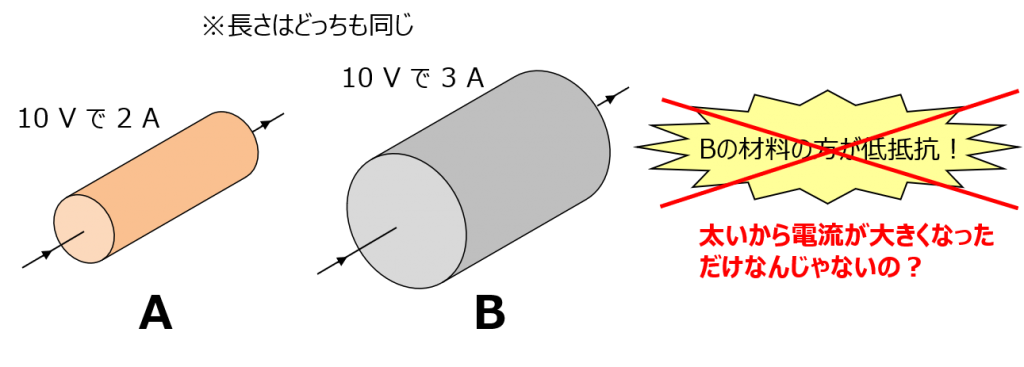
　例えば、長さが一緒で材料が違う2本の棒があったとするわね。片方を材料A、もう片方を材料Bとするわよ。この両方に 10V の電圧をかけて、Aの方は2アンペア、Bの方は3アンペアだったとしましょうか。Aの棒は 5オーム、Bの棒は 3.33オーム ってことになるけど、太さが違うのに「Bの方が抵抗が低い材料なんだ！」っていうのは不公平でしょ？
　Aからすれば、「お前は太いから電流がたくさん流れただけだ！」ってことになる。だから、材料としての抵抗の大小を比べたいなら、面積も考慮しなきゃいけない。

　という訳で例として、A は 0.03m²、B は 0.06mm² だったとしましょうか。抵抗値はそれぞれ 5オーム と 3.33オーム だったけど、これに面積を掛けるか面積で割るかの二択になる。
　で、今やってるのは、「材料としての抵抗の大小の比較」。そしてさっきBに対して、「お前は太いから電流がたくさん流れただけだ！」ってイチャモンを付けた。計算しようとしている指標は、「値が小さいほど大きな電流を流すことができる」ものだから、面積が広いことによる有利(材料の実力とは関係ない要素)を打ち消すためには、面積の数字を掛けてあげるのが正解。面積で割っちゃったらBの方は余計に小さくなって格差が広がるでしょ？

　だから棒としての抵抗値に面積を掛けるわよ。それぞれ計算すると、

A：5 × 0.03 = 0.15 [Ω·m²]

B：3.33 × 0.06 = 0.2 [Ω·m²]

になるわ。だから材料として抵抗が小さいのはAの方よ。検証してみるけど、同じ電圧(10V)をかけた時に流れた電流が、Aは2アンペア、Bは3アンペア だった。BはAの1.5倍の電流が流れたけど、そもそも面積が2倍だった。つまりBは、2倍の面積がありながら1.5倍の電流しか流せなかったことになって、材料としての抵抗は A よりも大きいことになる。という訳で A の勝利！　大逆転おめでとう！

　長くなっちゃったけど、どっちの方が材料として抵抗が小さいものなのかっていうのは、抵抗率で比べなきゃダメなの。さっきの棒の例は長さを揃えたから [Ω·m²] で比べたけど、長ささえも考慮するなら、[Ω · m² / m] = [Ω · m]。だけど、いかに短く作るかさえも競争の対象にする時には [Ω·m²] のまま比べちゃうこともあるわ。

　あと最後、抵抗率の単位は状況によっては [Ω· cm] が使われることもあるけど、これは 1メートル が 100センチ なのと同じように、

1 [Ω· m] = 100 [Ω·cm]

になるわよ。だけど抵抗率を Ω·cm のまま使おうとしたら、長さと面積も cm と cm² でやんなきゃいけなくなるから注意してね。いっそのこと全部 Ω· m と m と m² に変換してから計算するのも1つの手よ。

　抵抗率については以上よ。導電率の逆数ってだけだけど、抵抗を考える上ではこっちを使った方がやりやすいからよく使うわ。面積とか長さとの関係がゴッチャにならないように気を付けてね。