電圧と電流にまつわる単位の説明が終わったところで実際に何アンペア流れるかの計算に入って行くけど、「電荷の移動」を軸に話を進めていくからまずは導電率よ。これは電気伝導率とも呼ばれるもので、電流の流れやすさを示すものよ。
前回、電荷は電界から力を受けるって言ったけど、空気とか真空だったから動けなかった。金属があってようやく動けるんだけど、その時、導電率が大きいほど速いスピードで移動して行けるのよ。
単位はジーメンス毎メートル(S/m)って言うんだけど、今は気にしないで。ジーメンスっていうのも電流の流れやすさの単位なんだけど、その話はまた後で。
導電率は、材料ごとに値が決まってるわ。資料によってまちまちなんだけど、20℃の銅だと5900万 S/m ぐらいよ。「20℃の」って書いたのは、温度によっても変わるから。
20℃っていう前提で他の材料を書くと、銀が一番大きくて6140万、鉄だと桁落ちして990万になったりするわ。それでもすごいデッカい数字だから、巷で売ってある抵抗器は合金を作ったりして導電率の低い材料にしてるのよ。
そんな訳で、金属中の電荷の移動を考えていくわね。金属の電気伝導における電荷の担い手は、電子よ。金属原子にある電子の一部は原子核からの束縛が弱くて、電界から力を受けると移動することができるの。これを「自由電子」と呼ぶこともあるわ。これからは「電子」としか言わないけど自由電子のことだと思ってね。
ここでまた、5メートルの棒にご登場いただくわ。今回は立体的に円柱型でいくわね。材料は、そうねえ、普通の金属だと電流がめっちゃデカくなるから、オリジナルで 250 S/m の材料を作ったことにするわ。私ってば天才だからできちゃうの。今度は棒の面積も考えなきゃいけないから、これは0.08m2 にするわね。円だと半径16センチぐらいよ。あとこれは「断面積」って呼び方をして、電流の向きと垂直な面で考えなきゃいけない。
という訳で、この棒に 10V の電圧をかけるわよ! まず、この棒の中には 2V/m の電界が発生するわ。左の方が電位が高いから、電子は右から左に向かって移動する。だけど電子はマイナスの電荷を持ってるから、電流としては右に向かって流れてることになるわ。
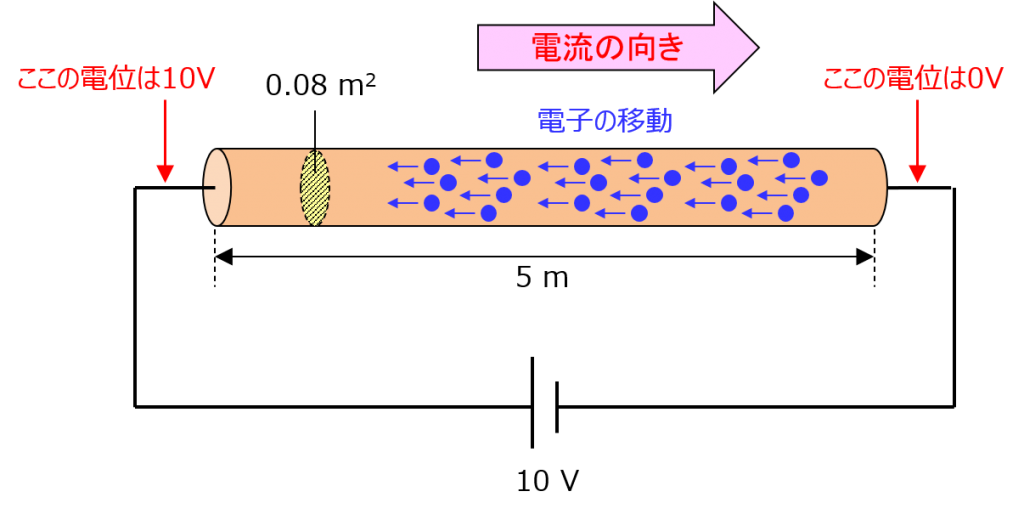
これで何アンペアの電流が流れてるのかを考えるけど、電流は、1秒当たりに通過する電荷のことだったわね。つまり、こう!
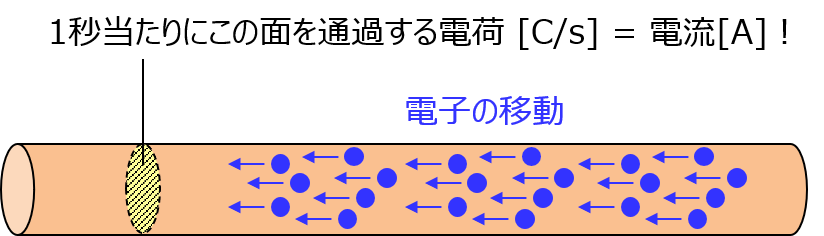
電荷の移動に対して垂直ならどこでもいいんだけど面を1つ定義して(上の図では黄色く塗ったわ)、その面を通過する電荷を考えればいいわ。電子1個が持ってる電荷の大きさは 1.6 × 10-19 クーロンって決まってるから、1秒当たりに通過する電子の数が分かれば電流も分かるわよ!
という訳で、1秒当たりに通過する電子の数を考えていくわね。まず考えるのが、そもそもこの棒の中にはいくつの電子(正確には自由電子)があるのか? っていうこと。
本来なら原子量だとかモルだとかで考えなきゃいけないんだけど、その話をするとかなり脱線するから数字でポンと与えちゃうわね。1立方メートル当たり 4 × 1026 個にしましょう。鏡子ちゃんお手製のオリジナル材料だからその辺は私の自由よ。単位をつけて書くなら、4 × 1026 [ m-3 ]。「毎立方メートル」って読んでね。10の26乗だからかなりデカいけど、5メートルの棒の中の、超ミクロな電子の数だからメッチャ多いのよ。
この数字に体積を掛ければ棒全体の中の電子の数がわかるけど、実は1立方メートル当たりの数の方をこの先の計算で使うから、このままにするわ。この、1立方メートル当たりの電子の数を、電子密度って呼ぶわよ。
次に考えるのが、電子の移動スピード。1秒当たりに通過する電子の数を求めなきゃいけないからね。
物質中での電子の移動を考える時、実はミクロな粒子同士の衝突でストップしては電界に引っ張られてまた加速するのを繰り返すんだけど、電子の数はウジャウジャで衝突のタイミングもまちまちだから、平均スピードで考えるわよ。この平均スピードのことを「ドリフト速度」って呼ぶわ。単位は普通にメートル毎秒(m/s) よ。
このドリフト速度を v とすると、その大きさは次の式で求めることができるわ。
v = μ·E
また新キャラが出たわね。Eは電界のことだけど、μ(ミュー)は移動度っていうやつよ。これも材料ごとに決まってるわ。だから数字でポンッと与えちゃうけど、3.9 × 10-6にする。単位は [ m2 / (V·s) ] なんだけど、v が [m/s] で E が [V/m] だから次元の逆算でこうなってるの。
移動度は、与えた電界に対する電子の移動スピードを示すためのパラメータだと思えばいいわ。これが大きい材料を使うと、電子の移動スピードがアップするの。
そんな訳で、移動度は材料で決まってるから電界強度さえ分かればドリフト速度が計算できるわね。5メートルの棒に 10V かけるから電界強度は 2 V/m で、ドリフト速度は、
v = μ·E = (3.9 × 10-6) × 2 = 7.8 × 10-6 [m/s]
になるわ。7.8 の100万分の1だから超おっそいけど、導電率が250しかない抵抗体だとこんなもんよ。(銅の導電率は5900万ね)
さて、1m3当たりの電子の数(電子密度)と、電子が移動する平均スピード(ドリフト速度)が分かったから、1秒当たりに通過する電子の数と、電流も計算できるわよ? もっかい図を乗せると、こうなるわ。
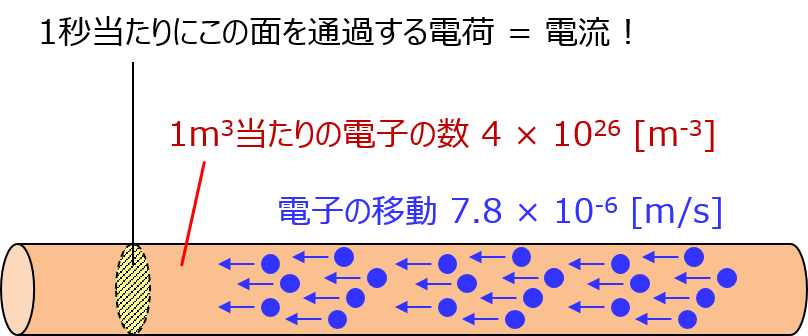
ここから1秒当たりに黄色い面を通過する電子の数を考えるけど、「1秒当たりに通過する電子の数」っていうのは、「1秒待ってる間に、どこにいる電子までが黄色い面に辿り着けるか」を考えれば いいわ。改めて描くと、こうね。
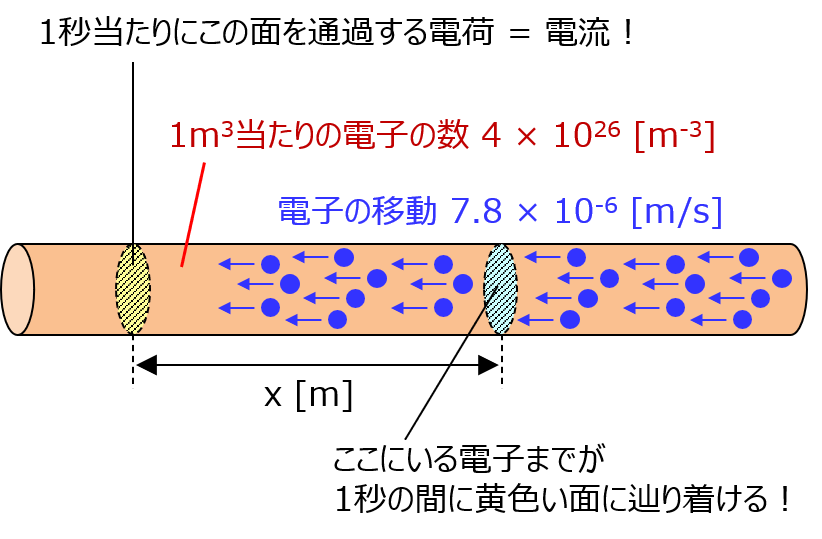
例えば、近くにいる子は0.1秒もかからずに来る。0.5秒ぐらいで来る子もいれば、1秒ギリギリになって来る子もいるわ。そのギリギリの地点までの距離を x としましょうか。青い面の位置よ。で、青い面より右にある子は1秒以内に来れないから電流計算に加われない。つまり、黄色い面と青い面に挟まれた区間にある電子の数が、「1秒当たりに通過する電子の数」よ!
棒の断面積は 0.08m2 だからそれに x を掛ければ黄色と青で挟まれた区間の体積になって、それに電子密度 (4 × 1026 m-3 )を掛ければ「1秒当たりに通過する電子の数」になるわよ! だから、x が分かればいい!
で、その x だけど、実はもう分かってる。勘のいい人なら気付いてるかしら? 黄色い面まで1秒で来れるギリギリラインであるこの x、これがドリフト速度 v とまんま同じ数字になるわ。だって、v の単位はメートル毎秒、「1秒当たりに進む距離」だから。つまり、
x = v · 1 = 7.8 × 10-6 [m]
「かける1」っていうのを強調したのは、「速度 v に時間1秒をかけました」って意図を示すためよ。x と v は次元が違うから、「x = v」っていう書き方をしちゃ絶対ダメよ。私が先生だったらそれだけで減点するわ。
x が分かったから、黄色と青で挟まれた区間の体積と、1秒当たりに通過する電子の数も分かるわね。電子密度と、断面積と x の積よ。その数を y とすると、
y = n·A·x = (4 × 1026 ) · 0.08 · (7.8 × 10-6) = 2.496 × 1020
になるわ。単位を書いてないけど [個] だから無次元よ。n が [m-3] で A が [m2] で x が [m] だから、打ち消し合って消えちゃうの。で、確かにこの y は「1秒当たりに通過する電子の数」なんだけど、無次元だと「1秒当たり」を強調できないから、距離 x の代わりにドリフト速度 v を使って計算するわね。だって v は、「1秒当たりに」進む距離のことだから。
つまり! 1秒当たりに通過する電子の数を z とすると!
z = n·A·v = (4 × 1026 ) · 0.08 · (7.8 × 10-6) = 2.496 × 1020 [s-1]
これで単位が [ 個 / s ] になったわ。普通は「個」ってのは書かないから [s-1] よ。x とか y は、あくまで考え方を示すために導入したものよ。物理の世界ではね、「1秒当たり」って言うからには単位に「毎秒」が入ってなきゃいけないの。今回、x と y と z で単位がバラバラだから気を付けてね。
さあ、最後、ついに電流を計算するわよ。電流は、1秒当たりに通過する電荷 [C/s] だから、電子1個が持ってる電荷 [C] と、1秒当たりに通過する電子の数 [s-1] の積よ。
I = q·z = (1.6× 10-19) · (2.496 × 1020) = 39.9 [A]
やっと電流が求められたわね。39.9A よ。導電率250の材料でさえ 10V で 40A になっちゃうんだから、何百万とか何千万もある金属に 10V を直接かけたらどうなるか、分かるわよね。何百万アンペアって電流を出せるパワーを持った電源がそうそうないんだけど、もしあったら一瞬で「パァン!」とか鳴って色々とブッ壊れるわ。だから電位の異なる金属同士を接触させちゃダメよ。最近は保護機能付きの電源も多いけど、過信しないように。私のビジネスの出先でどっかのアホがやらかして瞬停して騒ぎになったわよ!
ようやく電流が求められたところで、たくさん出て来たパラメータをおさらいするわね。まず、いかなる時も変わらないのが、電子1個が持ってる電荷。
q = 1.6 × 10-19 [C]
次に、棒を1本持って来たところで決まってるのが、下の5個。
長さ :L = 5 [m]
断面積 :A = 0.08 [m2]
導電率 :σ = 250 [S/m]
移動度 :μ = 3.9 × 10-6 [m2 / (V· s)]
電子密度:n = 4 × 1026 [m-3] ← [ 個 / m3 ] のことよ
次。この棒に10Vの電圧をかけるって決めたから、
V = 10 [V]
ね。これから計算に入るけど、まず、電子の平均移動スピードであるドリフト速度 v が欲しい。これは、
v = μ·E = μ · ( V / L ) = 7.8 × 10-6 [m/s]
になった。計算の過程は書くと長くなるから省略するわね。次に、電子が黄色い面まで1秒で来れるギリギリの距離 x を計算したわね。
x = v · 1 = 7.8 × 10-6 [m]
次が1秒当たりに通過する電子の数だったけど、まずは [個] だけの単位で、
y = n·A·x = (4 × 1026 ) · 0.08 · (7.8 × 10-6) = 2.496 × 1020
だったわね。だけど物理の世界ではこれを「1秒当たり」として扱うことができないから、単位に「毎秒」が入るように、距離 x の代わりに 速度 v を使って、y とは別のパラメータ z を計算した。そしてその z は、
z = n·A·v = (4 × 1026 ) · 0.08 · (7.8 × 10-6) = 2.496 × 1020 [s-1]
だったわね。[s-1] がしっくりこない人は [個/s] だと考えればいいわ。そして最後、電流は1秒当たりに通過する電荷(クーロン毎秒)のことだから、「電子1個が持ってる電荷」と「1秒当たりに通過する電子の数」の積で、
I = q·z = 39.9 [A]
になったわ。これを1つの式にまとめると、
I = q· z
= q · n · A · v
= q · n · A · μ · E
= q · n · A · μ · V / L
になるわ。σ がいねぇ! ってなるけど、実は導電率 σ は、
σ = q · n · μ
って定義されてるの。μ も n も材料ごとに決まってて、q も 1.6 × 10-19 クーロンって決まってるから、導電率は材料ごとに決まるのよ。今回は私のオリジナル材料だったから移動度も電子密度も適当に与えたけど、実はこの関係が崩れないように調整してたの。
導電率は電流の流れやすさを示すものだから、もし q が大きくなったら、電流はクーロン毎秒のことだから当然大きくなる。n は電子密度だから、これが大きいと電子が多いってことだから当然ね。そして μ は移動度。1 V/m の電界を与えたときの電子の移動スピードを示すものだから、これが大きくなると通過する電子の数が増えるから、電流も大きくなるの。
そんな訳で σ = q · n · μ を上の電流の式に代入すると、
I = σ· V· A / L
になるわ。随分と簡単になったわね。この式の意味するところは、
●導電率が大きいと電流は大きくなる(上に書いた通りよ)
●電圧が大きいと電流は大きくなる(棒の内部に発生する電界が強くなって、電子の移動スピードが上がるからよ)
●断面積が大きいと電流は大きくなる(単純に、電子の通り道が広くなって通過する電子数が増えるからよ)
●長さがあると電流は小さくなる(電圧固定のまま棒だけ長くなると電界が弱くなるからよ)
って感じよ。電荷の移動こそが電流で、電荷は電界から力を受けて動くってことが、全部この式に入ってるわね。
さて、この流れでもうやっちゃうけど、与えた電圧に対して流れる電流の計算には、抵抗をよく使う。知ってる人も多いと思うけど、棒状の物体が持ってる抵抗っていうのは簡単に計算できて、
R = L / ( σ · A )
になるの。そして、抵抗の逆数(1/R)を考えると、
1 / R = σ · A / L
になって、これを I = σ· V· A / L に代入すると、こうなるわ。
I = V / R
ようやく辿り着いたわね。オームの法則よ。式としては単純に与えられてるけど、電荷の移動こそが電流だから、物体の中に電子がいくつあってどれほどのスピードで動いてるのかっていうのを突き詰めていくと、これまで話してきたような内容になるの。これさえマスターすれば、あなたはもうオームの法則で迷わないわ。難しいけど、頑張ってね。
~column~
今回、計算の途中で移動度っていうのが出て来たわよね。あれは材料ごとに決まってるものなんだけど、実はまだ細かい式があるの。これよ。
μ = τ · q / m
また新キャラが出たけど、τ(タウ)は、平均自由時間ってやつで、ドリフト速度の説明で「電子が移動中にミクロな衝突でストップしてからまた加速する」って言ったわよね。その、衝突から次の衝突までの時間の平均のことよ。緩和時間とも呼ばれるわ。
qは、電荷。電子なら1.6 × 10-19 クーロンね。
mは、電子の有効質量。「有効」って文字がついてるのは、真空中で止まってる時の質量とは違う質量を持ってるように振る舞うことがあるから、計算ではこっちを使うようにするために「有効質量」って呼び方をするの。
平均自由時間が長いほど衝突が少ないから移動度は上がって、物体は質量が大きいほど動かしにくくなるから m は分母にあるのよ。余裕のある人は覚えててね。