さぁ天才鏡子ちゃんによる電気講座のスタートね? でもまず電気の話に入る前に、単位についての話をするわ? メートルとかキログラムという、あれよ。単位ってのは長さ1つを取ってもメートルとか尺とかヤードとか色々あるんだけど、世界全体で統一しましょうっていう動きからできたのが国際単位系、SI (Système International d’unités:フランス語由来)よ。で、このSIで使われてる単位のことをSI単位と呼ぶわ。
SI単位の特徴は、たった7つの基本単位の組み合わせで全てのSI単位を表せるってところにあるわ。SI単位なら、7つの基本単位のかけ算と割り算だけでできてしまうの。じゃあ7つの基本単位って何だよって話だけど、下の表の通りよ。それぞれの「1」の基準になる定義もちゃんとあるんだけど、まどろっこしいから省略するわ。
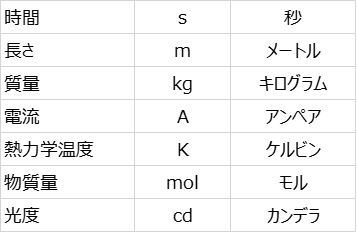
これがSI基本単位のラインナップよ。知ってるって人もいれば、ボルトとかニュートンがないじゃんって人もいるかしら。でも、ボルトもニュートンも上の表の子たちの組み合わせでできちゃうのよ。覚えなくていいけど、ボルトはキログラム×平方メートル÷(秒の3乗×アンペア)で、ニュートンはキログラム×メートル÷秒の2乗よ。式で書けば、
[V] = [ kg · m2 / (s3· A) ]
[N] = [ kg · m / s2 ]
になるわ。あ、ニュートンの方は覚えてていいかも。私が大好きな運動方程式(ma = F)まんまだから。mが質量[ kg ]、aが加速度[ m / s2 ]、Fが力[ N ]ね。 いや力学じゃなくて電気の勉強してんだけどって人も、ニュートンは覚えといた方がいいわ。電気と力学には切っても切れない関係があるから。だって発電機って、物を回すことで電気が生まれるでしょう?
キログラム×平方メートル÷(秒の3乗×アンペア)だとか、キログラム×メートル÷秒の2乗だとか出て来たけど、これらのことを「次元」って言うわ。分かりやすいのは、メートルの2乗とメートルの3乗は文字通りの別次元ってとこかしら。
「2次元」とか「3次元」は日常会話でも使うけど、あれはあくまで「メートルの2乗」とか「メートルの3乗」って意味で、キログラムとかアンペアだとかも立派な「次元」なの。大事だから覚えといてね。
言い方としては、「ボルトの次元はキログラム×平方メートル÷秒の3乗÷アンペアと同じ」とか、「ニュートンの次元はキログラム×メートル÷秒の2乗と同じ」っていう風になるわ。この、「〇〇の次元は△△の次元と同じ」っていう表現は、たまに使うから頭の片隅に置いといてね。
さて、何で最初に単位の話をするかと言うと、とっても大事だからよ。単位のことを知らずにオームの法則だとかに挑戦するのは、無謀とまでは言わないけどオススメしないわ。次のステップに進む時に無謀な挑戦を強いられることになるから。 それじゃあ次回から1つ1つの単位について説明していくわね。最初は、SI基本単位にも選ばれてているアンペア、じゃなくて電磁気の礎たるクーロンよ。
~column~
たまに、こういった感じでコラムを書くわ。だけどちょっとレベルの高い話になるから難しければスルーしてね。
記念すべき初回のコラムだけど、本編中にも出て来た「次元」の話よ。電磁気に限らず物理学を扱う上ではとっても重要。このページを読んでる人たちは、「テストが近いけど分からない!」とか「仕事でやることになったけど分からない!」とかだと思うけど、そういった人たちの役に立つと思うわ。というかその辺を超えてガッツリ研究してる人たちには参考にならないと思う。
まず簡単な話から入るけど、次元の違う単位同士の足し算と引き算はできないわ。キログラムとメートルの足し算なんてできないよね。当たり前じゃんって話だけど、ちょー重要だから。電気の話をすると、アンペアとボルトの足し算はできないし、アンペアとオームの足し算もできない。だからどんなにパニクっても足し算しちゃダメよ。
テストの問題で与えられる数値の単位はそれぞれ別次元なことが多いから、基本はかけ算と割り算で突破して行くことになるわ。ここでたまに、本編では「覚えなくていい」って言った次元が、実は覚えとくと便利だったりするの。 オススメとしては、本編でも触れたニュートンと、次はジュールね。ジュールの次元は、キログラム×メートル2乗÷秒の2乗よ。どっかでみたような並びだけど、ニュートンにメートルを掛けただけよ。式で書くなら、
[J] = [ kg · m2 / s2 ] = [ N · m ]
ってところね。だからニュートンの次元と、[J] = [ N · m ]さえ覚えとけば何とかなる。
いきなりだけど問題!
有効落差120m、水の流量30 m3/s、諸々の効率95%の水力発電所の発電電力は何ワットになるでしょう!
いやいや、そんなん知らんわ。ってところかしら? 人によっては公式を知ってるわよね。これよ。
P = 9.8QHη [kW]
答えを言っちゃうと、9.8に120と30と0.95を掛ければいいわ。33516が出るから、33.5メガワットってところね。注意したいのは、公式をまんま使うとキロワットで出るから3ケタずれる。ちなみに一番右の変なマークはギリシャ文字の「イータ」よ。アルファとかベータとかのあれね。効率という意味で使われることが多いわ。
で、この水力発電の問題だけど、次元を極めてる人なら公式なくても解けるの。では一緒にやってみよー!
まず、水力発電というのは、高い所にある水の位置エネルギーを、流し込むことによって水車を回す運動エネルギーに変えて、それで発電機を回して電気エネルギーに変えてるわ。まずは導き出さなきゃいけない電気エネルギーに目を向けるけど、電力の単位・ワットの次元は、ジュール÷秒よ 。(さすがにこれは覚えて!) つまり、
[W] = [ J /s ] = [ kg · m2 / s3 ]
ね。ワットと言えば「ボルト×アンペア」だけど、上に出てるボルトの次元にアンペア掛けたらちゃんとこれになるわよ。
さて問題は、有効落差120m、水の流量30 m3/s、諸々の効率95%という与えられた戦士を使って電力を導き出すんだけど、どう考えても足りない。ちなみに効率に次元はないわ。効率は「出力エネルギー÷入力エネルギー」だから、分母と分子が同じだから打ち消されちゃう。こういうのを「無次元」って呼ぶわよ。
で、問題に取り掛かるけど、水車を回すのには水を流すけど、もちろん水車の回転速度が速い方が発電電力も大きくなるわ。回転速度を上げるには、より大きな力を与えればいい。じゃあ力は何で決まるのか? 有効落差と流量だけじゃないわよ? だってニュートンの次元は、
[N] = [ kg · m / s2 ]
だもの。キログラムがいる。メートルは3乗もいらない。分母の秒は2乗いる。でも問題文で与えられてないじゃん! って話だけど、そういう時は、与えるまでもなく自然に存在してるものが潜んでる。
まず1つは、上の公式に答えが書いてあるんだけど、重力加速度。「9.8」のやつね。ただ、問題文に与えらてない時は「9.81」を使って計算した方がいいわ。加速度の単位は[ m / s2 ]だから、材料が増えたよ!
でもキログラムねぇじゃん・・・。
という訳でもう1つ、問題文で与えるまでもなく自然に存在してるものが潜んでます。いや、厳密には与えられてる。そう、流し込む材料が「水」であること。力学を習ってなきゃ分かんないんだけど、力は質量に比例する。だから、流し込む材料が水から油に変われば、同じ流量で流したとしても水車に加わる力も、回転速度も変わるの。
上の公式を見て疑問に思った人もいると思う、なぜ出てくる数値の単位がキロワットなのか。 それは、質量の基準がキログラムだからじゃないわ。なぜなら、ワットの次元の中に質量は「キログラム」として入ってるから。普通は、キログラムで計算すればワットになる。
ではなぜ、上の公式はキロワットになっているのか。それは、水の1立方メートル当たりの質量が1000 kgちょうどだからよ。あの公式には、この1000が混ざってる。「1立方メートル当たりの質量」って言い方をしたけど、これを「密度」と呼ぶわ。単位は[ kg / m3 ]。そのまんまね。
キリのいいことに水の密度がちょうど1000だから、公式には見えてないだけなの。はっきりと言うわ。上に書いてる水力発電の公式、あのまんまで覚えるのは、かなり危険。中身を理解してないまま公式だけが脳ミソに染みついちゃうと後で大変なことになるわよ? 「なんか知らないけど勝手にキロワットで出るぜラッキー♪」とか思っちゃダメよ? 勝手にキロワットになっちゃう危険な公式なの。
という訳で、密度1000 kg / m3 の液体を、重力加速度9.81 m /s2 の惑星で、120mの高さから流し込みますと言うのが位置エネルギーよ。(実際、この3つの掛け算が[ J / m3 ]と同じ次元になるわ)
で、水路の角度とか面積で決まる実際の水の供給スピードが、「流量」たる30 m3 /s。これを水車にぶつけるよ! エネルギー変換効率はもう95 %って問題文に書いてあるから摩擦とかはそこに入ってる。
出揃った物理量を整理しよう!
・有効落差:120 m
・水の流量:30 m3/s
・水の密度:1000 kg / m3
・重力加速度:9.81 m /s2
・効率:95 %
で、これらを使って発電電力を導き出すわ。別次元同士の足し算はできないから掛け算か割り算。そして、力は質量にも加速度にも比例するし、位置エネルギーは有効落差に比例する。もちろん流量は速い方が水車に与えられる力も大きい。
という訳で全部かけ算だ!! 計算する前に検証してみましょ♪
[m] × [m3 /s] ×[ kg /m3] × [ m / s2]
= [ m5· kg / s3· m3 ]
= [ kg· m2 / s3 ]
上に出てるワットの次元と同じになったよ! 間違いないね! 効率を掛けるのを忘れなければ、33.6 × 106、つまり33.6メガワットになるわ。9.8を9.81にしたからちょっとズレたけど、計算の根拠をちゃんと書いてれば〇にしてくれるはずよ。公式使わなかったから減点とかいう教師がいたら、その人は教師失格だから心の中で見下しといて。
という訳で今回は、次元の力を使って水力発電の計算をやったよ! 重力加速度とか物質の密度とかいう概念を知ってなきゃいけないけど、その辺も含めて単位というのは重要なの。公式ってやつも色んな要素が絡み合ってできてるものだから、ただ使うだけじゃなくて中身もしっかり理解しておいてね。