電力や電力量の話でも出て来たエネルギーと「仕事」についてもここで話しておくわね? まず、エネルギーって何ぞって言うと、「仕事」をする能力のことよ。「仕事」は、物を動かすとか、あっためるとか、光や音を出すとかのこと。物体は、持ってるエネルギーの分だけ「仕事」をすることができるの。
エネルギーの単位はおなじみのジュールで、「仕事」の単位もジュールだった。じゃあそもそもエネルギーと「仕事」はどう違うのか? っていう疑問も湧いてくるわよね。
これは人よって解釈が変わったりもするんだけど、「エネルギー」は「所有あるいは消費するもの」で、「仕事」は、文字通り「働きかけるもの」ってところかしらね。
例えば、ボーリングの球を投げたとする。この時、転がってるボールは、その質量と速度に応じた運動エネルギーを持つことになるわ。「エネルギーを持つ」とは言うけど、「仕事を持つ」とは言わないわね。
同じように、高い位置にあるものは位置エネルギーを、温度のあるものは熱エネルギーを持ってることになるわ。電気エネルギーに「持つ」って概念を当てはめるのは難しんだけど、例えば、充電してあるバッテリーとかは「電気エネルギーを持ってる」と言ってもいいわね。実際にそれ使えばスマホが点くわけだし。てなわけで、所有に対しては、「○○エネルギーを持ってる」って言い方をする。この辺の言い回しで「仕事」は使わないわ。
じゃあ「仕事」は何かって言うと、「自身が持ってるエネルギーを消費して他の物質に作用する」ってところね。
もっかいボーリングに例えるけど、転がってるボールは運動エネルギーを持っている。それでぶつかったピンを吹っ飛ばす訳だけど、止まってる間は運動エネルギーがゼロだったピンが吹っ飛ぶ、つまり運動エネルギーを持つことになるから、これはボールに与えられたエネルギーってことになるわ。
運動エネルギーを得たピンはその場から動く。前にも言ったけど「物質を移動させること」は「仕事」で、実際、ボールがぶつかったピンは、他の外乱要因(壁にぶつかって反射するとか)がない限りは、元いた場所には絶対に戻らない。ピンは自身が得た運動エネルギーに従って動くから、「ピンが得た運動エネルギーの総量」が、「ボールがピンに対して行った仕事」と考えることもできるわよ。
現に、ボールは減速するから運動エネルギーを失ってる。ピンが吹っ飛ぶ運動エネルギーになってる他にも、ガコンって鳴る音エネルギーとか、多少は発生するであろう摩擦の熱エネルギーになる形でも失うわ。捉え方によっては、音や摩擦熱を発生させることも「ボールがやった仕事」だと言えるわね。もちろん、そのボールを投げて転がすのが、私たちの「仕事」。キーボードがヘコむのもカタカタ音が鳴るのも、「仕事」。世の中は全部、「仕事」でできてるの。
でもって電気エネルギーに関して言えば、「充電されてるバッテリーがトータルで行える仕事」が、「そのバッテリーが持ってる電気エネルギー」ってことになるわ。「バッテリーが行う仕事」っていうのが、スマホの駆動。最終的な出力で言えば、ほぼ光と音ね。使ってると熱を持つこともあるけど、あれはロスよ。ただ、ロスとして発生する熱も含めて「バッテリーが行う仕事」とも言える。
バッテリー容量はアンペア時で書かれることが多いけど、あれは電圧が3.7 Vで固定だから簡単にエネルギーに換算できるわ。ワット秒に直せばジュールと等価になるから、それが「フル充電のバッテリーが持つことになる電気エネルギー」ね。
電流のページで出たけど、スマホの駆動状態によって消費電力が変動して、最終的に電荷を使い果たせばバッテリー切れ。あのページにあるグラフで消費電力を時間積分すれば消費電力量、つまり消費エネルギーになるわよ。
熱はロスだって話をしたけど、そのロスを減らしたらどうなるかって言うと、消費電力が減って長持ちするようになる。熱くなるためのエネルギーを液晶とかスピーカーの出力に回せるようになるからね。だからバッテリー、熱くなるなよ!
これで電力とエネルギーに関する話は終わり。「仕事」だとかいう概念を持ち込んで申し訳なかったんだけども、この話をせずに電力の説明をするのは無理だったからコラムに送らずに入れさせてもらったわ。知ってた方がテストとかで問題解くとき行き詰まりにくくなるのは、マッドサイエンティストたるこの私が保証する。
電流とか電圧の話もそうだけど、単位のことを知らずに電気の勉強をするのがどんなに無謀かってことを分かってくれると嬉しいわ。
~column~
電気で動く道具ってのは、どうしても熱が発生してしまうわよね。せっかくだからその計算をしてみましょうか。
有り得ないシチュエーションかもだけど、ステンレス板の上に箱型の抵抗器が乗ってるとするわね。箱の中はニクロム線がぐるぐる巻きになってると思って。細かいことは気にしちゃダメよ。
で、これに電流を流すと発熱して箱の外側、つなりステンレス板や空気にも熱が伝わるわ。その状況で、この箱が何℃まで上がるか計算してみましょう。イメージは下の図で、あと計算しやすいようにいくつか前提条件を用意するわ。
■前提条件
・抵抗器の消費電力は全て熱になり、箱の外に出る。
・箱の表面や底面はどこでも全て同じ温度。
・箱とステンレス板は完全にくっついていて、箱の底面からステンレス板への伝熱でロスはない。
・下方向への熱は、最大45°まで横に広がる。
・ステンレス板の下には水冷板があり、ステンレス板の底面は25℃で保たれている。
・箱から遠く離れた場所の気温も、25℃。
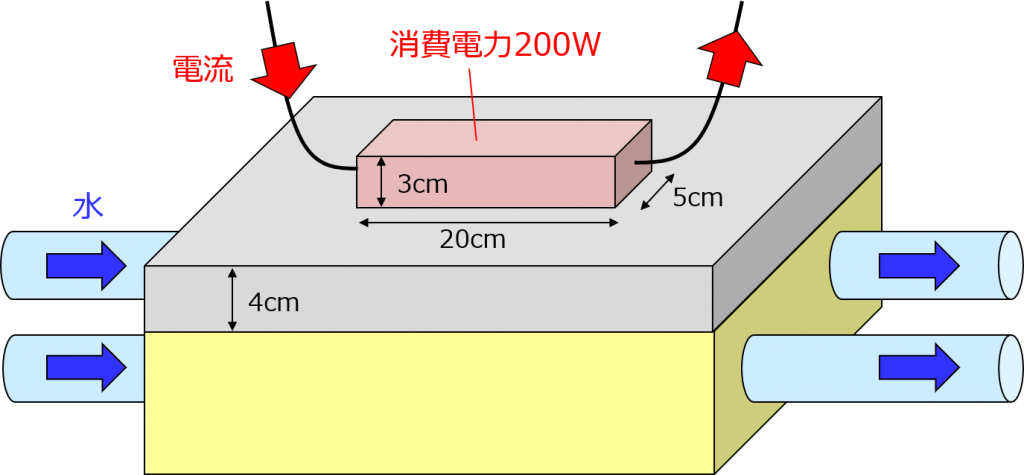
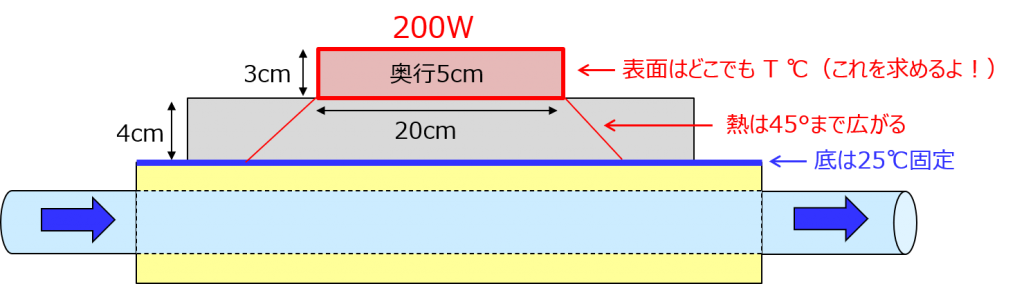
もはやどんな状況だよって感じだけど、これでやるわよ。まず、箱で発生した熱がたどる経路は、2つあるわ。1つは、下にあるステンレス板。熱いものに金属当てると、そいつまで熱くなるわよね。これを熱伝導(ねつでんどう)って言うわ。ステンレスの内側でも、上から下に向かって熱が移動していくわよ。これも熱伝導。要は、直接的な熱の移動ね。
もう1つは、箱の周辺にある空気。発熱体の周囲を気体や液体が漂っていると、そっちにも熱が吸われるの。これは熱伝達(ねつでんたつ)、あるいは対流と呼ばれる。空気や水にも熱伝導(ねつでんどう)はあるんだけど、それよりも熱伝達(ねつでんたつ)の方が大きく効くから、こっちで計算されることが多いわ。
で、これらの放熱経路がある中で箱の表面は何℃になりますかってのを計算するわよ。そのためには、熱抵抗ってやつを計算しなきゃいけない。これは、電気抵抗と似たような感じで、熱の移動をどれくらい妨げますかって言うやつよ。単位はなんと K / W(ケルビン毎ワット)。ずばり、これに発熱量(200W)をかけると温度差 ( T – 25 )が出て来るわよ。だから、熱抵抗さえ出せればほぼ終わる。
この熱抵抗を、ステンレス側と空気側のそれぞれで考えなきゃいけないから、ステンレス側を Rth_sus 、空気側を Rth_air としてやっていくわね。
まず、ステンレス側。箱の底から下に向かって熱が伝わっていく訳だけど、真下だけじゃなくて斜めに広がっていくわよね。でも限りなく真横まで行く訳でもないから、今回は45°までってことにしたわよ。
だけどいきなりそれで計算するのは難しいから、まずは、熱伝導計算のやり方を確認するために、真下にしかいかない前提でやってみるわ。図にすると、こう。後でちゃんと45°に広がるバージョンもやるから、安心してね。
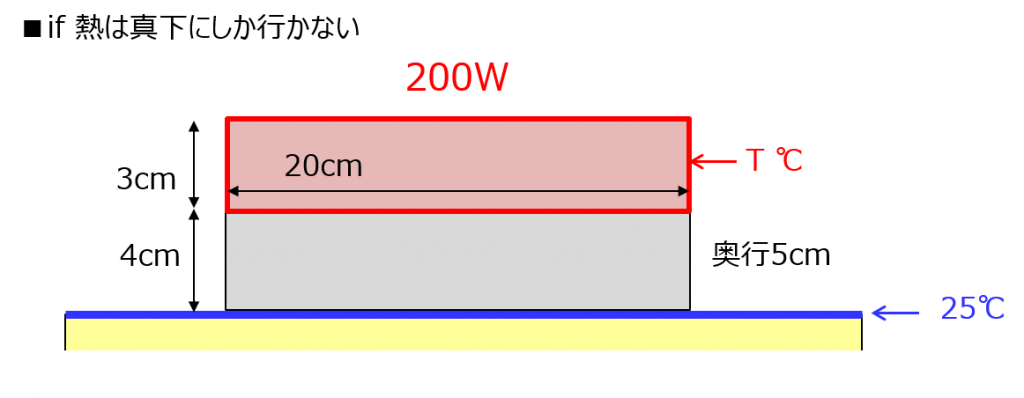
じゃあ早速、箱の底(ステンレス板の上面)からステンレス板の底までの熱抵抗を計算するわよ。これは、求めるための式がある。
Rth = d / (λ·A)
変なのが出て来たわね。「λ」は「ラムダ」って読むもので、熱伝導率っていうパラメータよ。電気でいうところの導電率と同じで、熱の伝わりやすさを示すものよ。物質ごとに値が決まってて、ステンレスは合金の配合によってマチマチなんだけど、今回は16 W / (m·K) ってことにするわ。このW / (m·K) が単位で、「ワット毎メートル・ケルビン」って読む。
次、dは、進行方向の距離。今回で言えば、ステンレス板の厚み、4センチね。んで、Aは進行方向に対する断面積。今回で言えば、幅20センチと奥行5センチのかけ算、平方メートルで出すと0.2 × 0.05 = 0.01 m2 になるわ。
そんな訳で、これで熱抵抗を出すわよ。
Rth = d / (λ·A) = 0.04 / ( 16 × 0.01 ) = 0.25 [ K / W ]
はい、終了。これが、熱伝導での熱抵抗の出し方よ。ついでに、仮に 200 W 全部がこっちに来る(空気に逃げる熱がない)っていう仮定のもとで続きをやるなら、
T – 25 = Q· Rth
になるわ。Qは熱流っていうやつで、移動する熱のことよ。単位はW(ワット)。今回は抵抗の消費電力が全部熱になるという前提だから、空気に逃げる熱もないとするならば200 Wがそのまま使えるの。それで計算すると、
T = Q· Rth + 25 = 200 × 0.25 + 25 = 75 [℃]
ってなって終わり。これが熱伝導の基本的な考え方なんだけど、空気への熱伝達なしでやるなら熱抵抗はわざわざ計算しないことが多い。T – 25 = Q· Rth の式で、TをT1に、25℃をT2に置き換えて、Rthも展開してみるわね。
T1 – T2 = Q· d / (λ·A)
λ· (T1 – T2) / d = Q / A
これで左右をひっくり返して、
Q / A = λ· (T1 – T2) / d
= – λ· (T2 – T1) / d
で完成。これがフーリエの法則よ。なんでわざわざマイナスを外に出したかっていうと、熱流には向きがあるから。熱は、温度が高い所から低い所に向かって行くから、進むにつれて温度が下がって行く。
「温度勾配」っていうのを考えるんだけど、出発地(箱の底)からの距離が離れるにつれて温度が下がる時、温度勾配は負であるとされる。今回の例だと、T2が25℃、T1が75℃、dが4センチだから ( 25 – 75 ) / 0.04 で、マイナス1250 ℃ / m が温度勾配ね。「勾配」を考えるときは、ゴールでの温度から出発地での温度を引かなきゃいけないのよ。
で、熱流はプラスになるから、式としては温度勾配の負を打ち消すためのマイナスが先頭に必要。要は、「熱は温度が高い所から低い所に向かって行く」っていう事実を式で表現しただけ。
上向きの矢印で熱流を定義すればステンレスの底を出発地と考えられるけど、その時は温度勾配がプラスだから熱流が負になる。熱流が負になるのがどういうことかって言うと、定義された矢印とは逆方向に実際は流れてるって意味よ。熱流を負として扱うのはメンドくさいから、普通は発熱源から離れる方向をプラスで定義するわ。
式本体の説明に入るけど、左辺は、熱流を断面積で割ったもの。熱流の密度ってことになるんだけど、熱流束って呼ばれるわ。小文字のqで書かれることが多いから、小文字だったら熱流束、つまりQ / Aのことを言ってるんだなと思えばいいわ。
右辺は熱伝導率と温度勾配の積になってるわね。つまり、熱流束の値は熱伝導率と温度勾配の積に一致して、向きは温度勾配と逆になるっていうのがフーリエの法則ってワケ。
これが熱伝導計算の基本よ。それが分かったところで、熱が斜めに広がるのと、空気にも逃げるパターンも考えていきましょうか。まず、斜め要素のステンレス板から。改めて図を描くと、こうよ。45°方向までしか広がらない前提だから、その外側はカットしたわ。
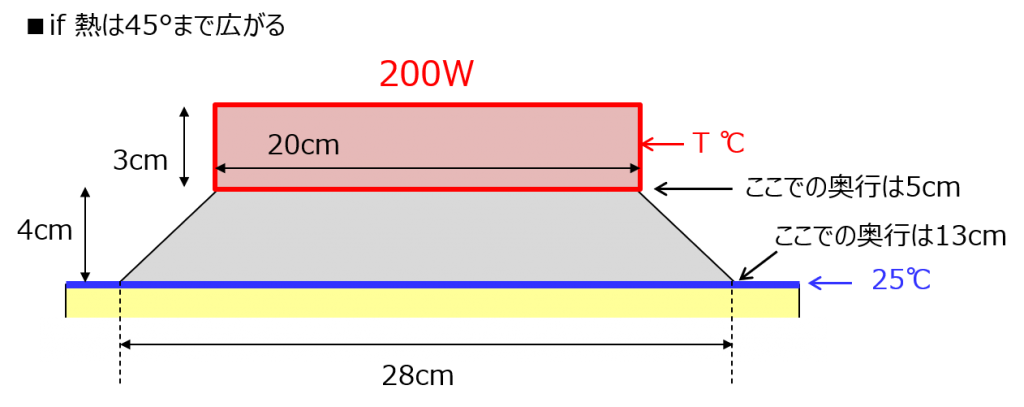
図を見た瞬間に嫌な予感がした人、いるでしょ。その予感、当たるわよ。熱抵抗はRth = d / (λ·A) っていう単純な式なんだけど、下に進むにつれて面積が広くなっていくから、一筋縄じゃいかない。
てなワケで、出発地、つまり箱の底からの距離を x として考えるわよ。箱の底が x = 0 で、ステンレス板の底が x = 0.04。でもって、ステンレス板を細かくスライスするわね。
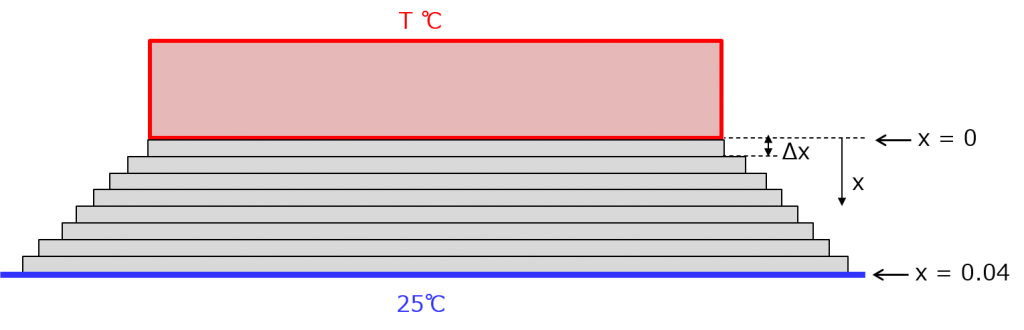
嫌な予感が、着実に現実味を帯びてきたわね。これでスライス1枚1枚の熱抵抗を全部足せば全体の熱抵抗になるわよ。
まず1枚目から面積を考えましょうか。これは、箱の底と同じ面積になるから、0.2 × 0.05 = 0.01 m2。次、2枚目。スライスされた板の厚みが Δx で、面積は45°方向に広がってるから x = Δx で、横幅は 0.2 + 2·Δx、奥行きも0.05 + 2·Δxになって、面積は ( 0.2 + 2·Δx ) ( 0.05 + 2·Δx ) よ。
同じように3枚目は、x = 2·Δx になるから、面積は ( 0.2 + 4·Δx ) ( 0.05 + 4·Δx ) になる。一番下のスライスは x が4センチなんだけど、ステンレス板の厚みを d と置くと、x = d だから面積は ( 0.2 + 2d ) ( 0.05 + 2d ) になるわよ。計算するのに欲しいのは任意の x での面積だから、これを Ax とすると、
Ax = ( 0.2 + 2x ) ( 0.05 + 2x )
になる。でもって任意の x での熱抵抗 Rth_x は、
Rth_x = Δx / ( λ · Ax )
= Δx / ( λ ( 0.2 + 2x ) ( 0.05 + 2x ) )
よ。進行方向は上から下だから、1枚当たりの熱抵抗を考える時、「距離」に相当する部分はスライスの厚みである Δx を使う。ここまで来るともう予感が確信に変わってるわよね。スライス全部の熱抵抗の合計、つまり、ピラミッドの下半分みたいな形になってるステンレス板の熱抵抗は、こうなる。
Rth_sus = ∫ Rth_x dx
積分キターーーーーーー!! あんたさぁ・・・。でも、積分を恨んじゃダメよ。積分があるからこそ、この問題を解くことができるのよ。てなワケで早速やりましょ。積分範囲はステンレス全体の厚みが4センチだから、x = 0から x = 0.04 までよ。
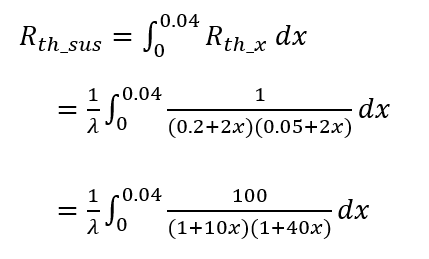
小数は鬱陶しいから外に出したわ。これは、
( 0.2 + 2x ) ( 0.05 + 2x )
= ( 0.2×( 1 + 10x ) ) × ( 0.05×( 1 + 40x ) )
= 0.2 × 0.05 × ( 1 + 10x ) ( 1 + 40x )
=( 1 + 10x ) ( 1 + 40x ) / 100
になるからこうできるのよ。で、100も積分の外に出して λ = 16 を代入すると、こうね。
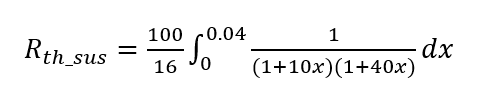
約分は後回しにするわ。さっそく積分に取り掛かるけど、分母が2次式になってる。これは、
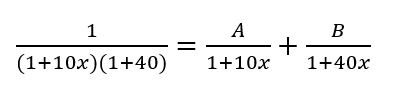
と置いて、これが成り立つようにAとBを導けば突破できるわ。右辺を取り出して計算すると、
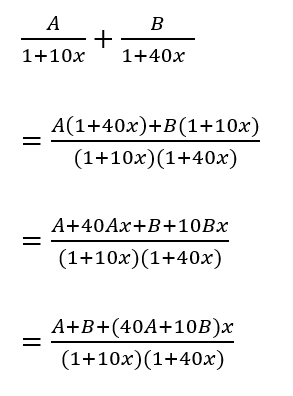
になる。これで分子が1になればいいのだから、
A+B = 1
40A + 10B = 0
の連立方程式ね。省略するけど、A = -1/3、B = 4/3 になるわよ。これで熱抵抗の計算に戻ると、
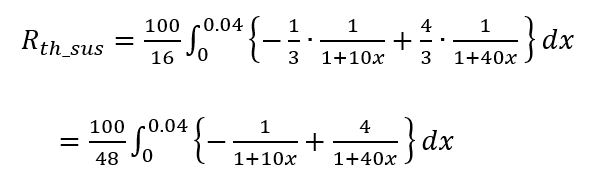
になる。1 / ( ax + b ) の不定積分は (– 1 / a)· ln | ax + b | + C だから、今回は ax+bの部分がプラスになるって分かってるからカッコで書くけど、
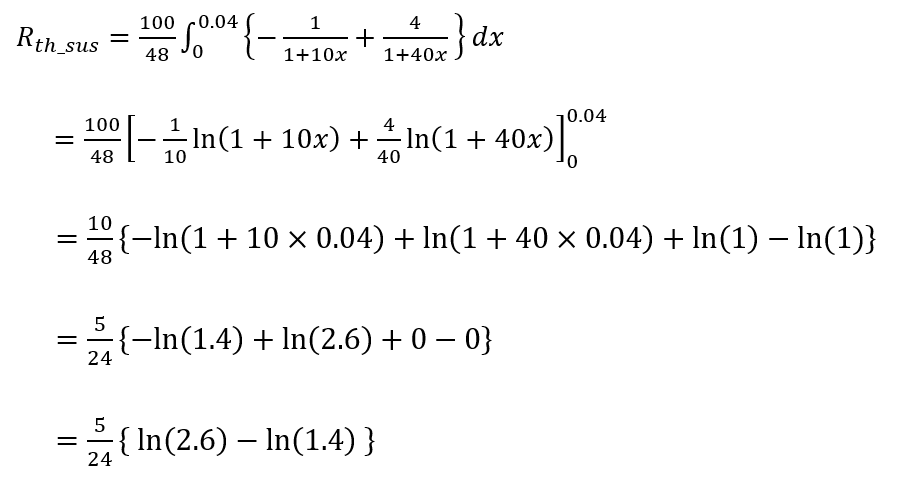
こうね。ここまで来たら後は電卓叩くしかないわ。関数電卓持ってない人は表計算ソフトとかでね。これを計算すると、
Rth_sus = 0.129 [K/W]
になる。やっと出たわね。
でもまだ空気側の熱抵抗が残ってるわよ? もうちょっとだから、頑張って! 今度は、ステンレスの方は無視して箱の表面を考えるわ。
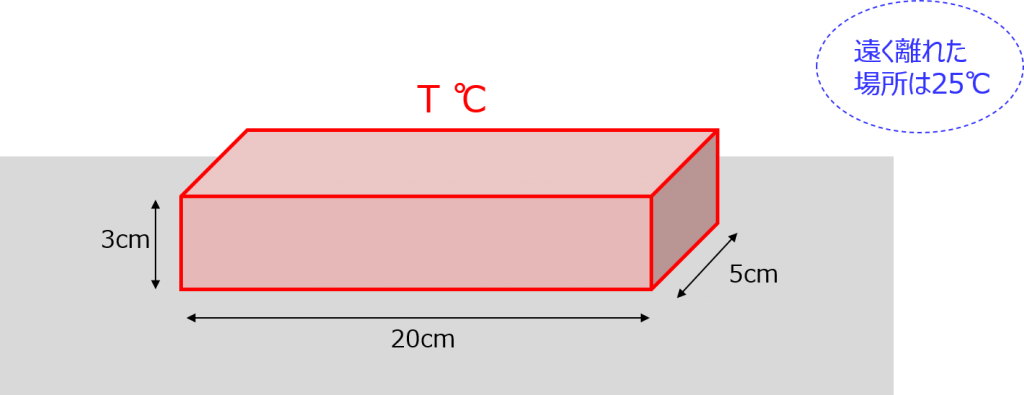
こういう図になるんだけど、熱伝達(ねつでんたつ)にも熱伝導(ねつでんどう)と同じように公式があるわ。こうよ。
Rth = 1 / ( h · A )
hっていうのは、熱伝達率(ねつでんたつりつ)。熱伝導率(ねつでんどうりつ)の熱伝達バージョンだと思えばいいわ。これが高いほど、周囲の気体(あるいは液体)に熱が伝わりやすい。
ただ、注意したいのが、これは物質ごとに決まってる訳じゃない。風吹いてるだけで何倍も変わる。扇風機があると涼しくなるでしょ? それと一緒。だから、熱伝達率は状況によって決まるものよ。今回は無風という前提で 5 W / (m2·K) にするわ。これが単位で、読み方は「ワット毎平方メートル・ケルビン」。
Aの方は面積なんだけど、これは空気と接触する面積。今回の場合は、底面を除いた5面の表面積よ。だから、
A = ( 3 × 5 × 2 + 3 × 20 × 2 + 5 × 20 ) × 10-4
= 250 × 10-4
= 25 × 10-3
になるわね。センチのまま計算して平方メートルに直すには、10のマイナス4乗よ。で、熱抵抗は、
Rth_air = 1 / ( h · A )
= 1 / ( 5 × 25 × 10-3 )
= 103 / ( 5 × 25 )
= 40 / 5
= 8
ってなる。
やっとこさ、ステンレス側と空気側の両方の熱抵抗が出たわよ! それぞれ、Rth_sus = 0.129 K/Wと、Rth_air = 8 K/Wになったわね。
後はこれをどうするかだけど、電気抵抗の並列回路と同じように考える。足し算しちゃダメよ。なぜなら、熱は下のステンレスと上の空気の両方に散らばるから。これらの経路は並列に存在するから、熱抵抗計算も並列になる。図にするとこうね。

これを熱回路と呼ぶわ。で、25 ℃の場所、かたや水冷版でかたや遠く離れた空気なんだけど、温度が同じである以上、熱回路上は短絡できる。つまり、こう。
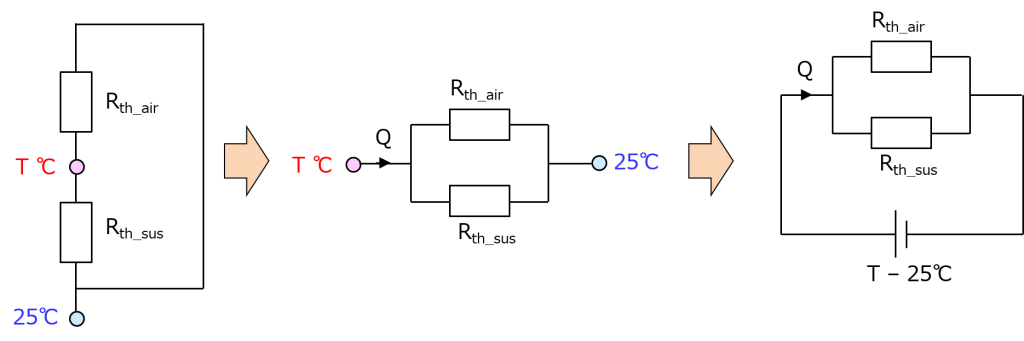
一番右に描いたように、温度差は、電気回路でいうところの直流電源(つまり、電位差)と同じ記号を使えるわ。後はこれで、電気回路と同じように合成抵抗を計算すればいい。2つしかないから「和分の積」ね。
Rth = Rth_sus · Rth_air / ( Rth_sus + Rth_air )
= 0.129 × 8 / ( 0.129 + 8 )
= 0.127
計算方法が一緒だから当然だけど、電気抵抗と同じように「小さい方の熱抵抗値」よりも小さくなる。つまりほとんどはステンレス側の熱抵抗で決まるってことね。これが何を意味するかって言うと、発生した熱の大半はステンレス側を通って放熱されるってことよ。
だから、よっぽど手を近付けない限りは熱を感じることはないでしょうね。いやコタツとかあったかいじゃんって思うかも知れないけど、コタツに水冷板なんてないのと、あれは、もうひとつの伝熱形態・熱放射が絡んで来るからまた話が変わる。
もちろん箱本体は熱くなるから、最後にその温度計算ね。
T = Q· Rth + 25
= 200 × 0.127 + 25
= 25.4 + 25
= 50.4
てなワケで、箱の表面温度は50.4 ℃よ。マジ、やっと終わったわね。最後の計算過程を見ての通り、25.4 の部分が温度上昇で、熱抵抗を下げればもっと小さくすることができる。風起こして空気側の熱抵抗下げるのも手だけど、ほぼステンレス側で決まるからアプローチとしてはそっちね。
簡単な方法は、熱伝導率の高い材料を使うこと。今回は 16 W / m·K のやつにしちゃったけど、よく使われるのはアルミとか銅で、アルミは230オーバー、銅はほぼ400とケタ違い。銅の方が性能がいいんだけど、コストとか重さが気になる時はアルミで妥協するって感じね。
ほとんど熱計算になっちゃったんだけど、電気器具っていうのはどうしても発熱しちゃうから、熱設計も重要なのよ。みんなもそれをやる日が来るかも知れないから、その時はまたここに来てね。