一次試験
理論

問題文に筋書きがある中での穴埋めだから、やりやすかったかも。
問1
(1)
△AOBと△BOA’が相似とするためのx座標をx’とすると、
x’ : a = a : d
が成り立つ。なので、
x’ = a2 / d
(2)
点Aにある電荷Qが点Bに作る電位は、AB間の距離がRなので、
VB = Q / (4πεR)
(3)
導体球は接地されているため、点Bの電位はゼロでなければならない。このため点A’にある電荷Q’が作る電位で打ち消す必要がある。まずB-A’間の距離を考え、それをR’とすると、△AOBと△BOA’が相似であるため、
R’ : a = R : d
が成り立ち、
R’ = a/d * R
となる。電荷Q’が作る電位は、大きさはVB1と等しく符号が逆転している必要があるため、
Q / (4πεR) = – Q’ / (4πεR’)
Q / R = – Q’ / R’
Q’ = – Q * R’ / R
= – Q * (a/d * R) / R
= – Q * a/d
(4)
x = -d の位置に -Q の電荷を置く場合も考え方は同じで、影像電荷を置く場所x’は
x’ : a = a : -d
が成り立つようにして
x’ = – a2/d
(5)
導体球上の電位がゼロなる条件を満たすように2つの電荷が置かれるので、導体球に誘起される電荷もゼロ
問2
(1)
磁束はインダクタンスと電流の積なので、x=0の時の磁束は、L(0)I
(2)
エネルギーは、1/2 * L(0) * I2
(3)
磁束がL(0)I のままインダクタンスがL(x)に下がるので、その時の電流を i(x) とすると、
L(x) * i(x) = L(0) *I
i(x) = L(0) / L(x) * I
(4)
エネルギーは、
1/2 * L(x) * i(x)2
= 1/2 * L(x) * L(0)2/ L(x)2* I2
= 1/2 * L(0)2/ L(x) * I2
(5)
分からなかったので適当にやりましたが、今思えば L(0) > L(x) なのでエネルギーは大きくなってるため、コイルに蓄えられる以外に考えられませんね。
問3
結局テブナンの定理を使いこなせる気がしなかったので重ね合わせの理でやりました。なので先にR1に流れる電流 I1が求まります。
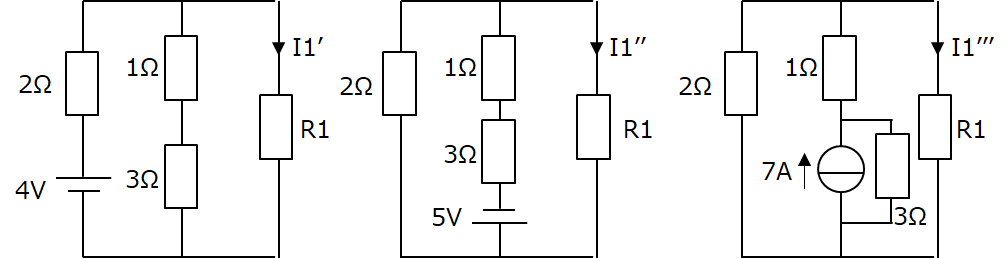
これで I1’ と I1’’ と I1’’’ を全部足せば I1 です。その結果、
I1 = I1’ + I1’’ + I1’’’
= 8/(4+3R1) – 5/(4+3R1) + 21/(4+3R1)
= 24 / (4+3R1)
になりました。これでテブナンの定理を使った等価回路のEとRを考えにいきます。
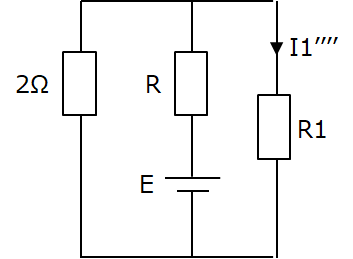
この回路で I1’’’’ を求めると、
I1’’’’ = 2E / ( 2R + (2+R)R1 )
になります。また、これが上の方で出した I1’’ と I1’’’ の和に等しくなるので、
I1’’’’ = I1’’ + I1’’’
= – 5/(4+3R1) + 21/(4+3R1)
= 16/(4+3R1)
です。したがって、
2E / ( 2R + (2+R)R1 ) = 16 / (4+3R1)
EとRの2つを求めなければならないことに対して式が1つしかありませんが、
2R:(2+R) = 4:3
が成り立たないと上の等式は成り立たないので、これでRが出せます。
2R * 3 = 4 * (2+R)
R = 4
これを代入すると、
2E / (8+6R1) = 16 / (4+3R1)
E / (4+3R1) = 16 / (4+3R1)
E = 16
となります。これで(1)~(3)までの答えが出揃いました。
(4)
なぜかは忘れてしまいましたが、こういう時は R1 = 4/3 Ω の時に消費電力は最大になります。
(5)
P = I12 * R1
= 24 / (4+3R1) * R1
=24 / (4+4) * 4/3
=12
問4
(1)
コンデンサを流れる電流は、コンデンサにかかっている電圧の微分値と静電容量の積なので、
i(t) = C * dv(t)/dt
直列なのでこれが抵抗にも流れるため、抵抗rでの電圧降下は、
vr(t) = i(t) * r
= rC * dv(t)/dt
キルヒホッフの第二法則より、
E = vr(t) + v(t)
= rC * dv(t)/dt + v(t)
(2)
微分方程式の解き方は色々ありますが、個人的に一番楽な手段、ラプラス変換を使いました。Eのラプラス変換はE/sで、dv(t)/dt はs*V(s) + v(0)で、v(t)はそのままV(s)となり、
E/s = rC * ( s*V(s) + v(0) ) + V(s)
E/s = V(s) * ( rCs + 1 ) + rCv(0)
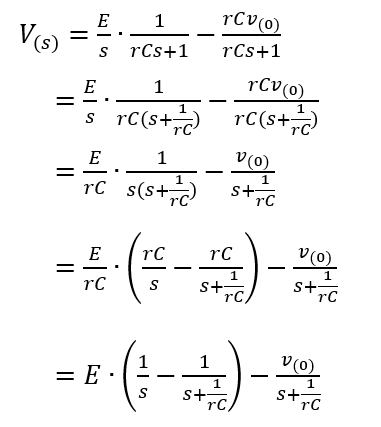
これをラプラス逆変換すれば、v(t)が求まります。1/sの逆変換は1で、1/(s+a) は e-at になるので、
v(t) = E * (1- e-t/rC ) – v(0) * e-t/rC
この時、時定数は rC です。
(3)
上記の v(t) の式で、E がそのまま v(∞) になります。スイッチを入れてしばらくすると、E は全てコンデンサにかかり、r には電圧がかからなくなります。コンデンサに遮られるので、電流も流れなくなります。あくまで充電中のみ、電流が流れます。
(4)
初期値がゼロと与えられたので、
v(T) = E * (1- e-T/rC )
v(2T) = E * (1- e-2T/rC )
これらの比は、
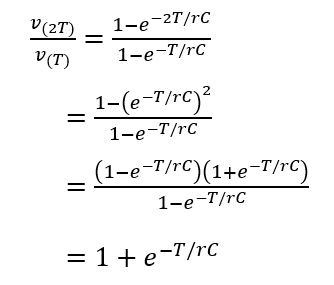
(5) 上の式でちょっと移項作業をすると、
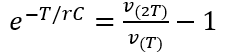
改めてv(T) を計算すると、
v(T) = E * (1- e-T/rC )
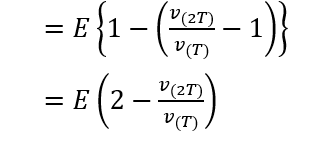
問5
(1)
有効電力600W、力率0.6の負荷の無効電力は800var
600 / 0.6 * √(1-0.62) = 800
(2)
抵抗成分3Ω、力率0.6の負荷のリアクタンスは4Ω
3 / 0.6 * √(1-0.62) = 4
(3)
RL直列負荷と並列にキャパシタを接続して総合力率を1にした時、
ωC = ωL / ( R2 + (ωL)2 )
になる。ωCの値を求める問題なので、
ωC = ωL / ( R2 + (ωL)2 )
= 4 / ( 32 + 42 )
= 4 / 25
= 0.16
(4)
上記の状態からωを1/2倍すると、ωC = 2/25、ωL = 2になる。したがって合成アドミタンスは、
Y = R / ( R2 + (ωL)2 ) + j ( ωC – ωL / ( R2 + (ωL)2 ) )
= 3 / ( 32 + 22 ) + j ( 2/25 – 2 / ( 32 + 22 ) )
= 3 / 13 + j ( 2/25 – 2/13 )
= 3 / 13 – j * 24 / (25*13)
力率は、
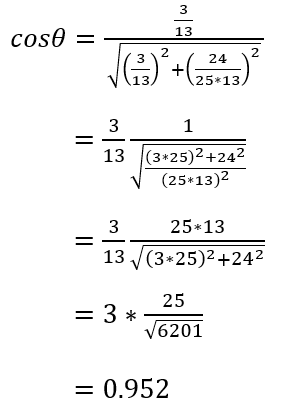
(5)
アドミタンスの虚部が負 (ωC < ωL / ( R2 + (ωL)2 ) ) なので、誘導性
問6
(1)
なんとなく名前を覚えてた
(2)
一番上の点の電位をVUとすると、
VU = E / 2
ΔR1とR1の間の電位をVLとすると、
VL = E * R / ( R1 + ΔR1 + R )
ブリッジ出力電圧は、
Vo = VU – VL =
= E * ( 1/2 – R / ( R1 +ΔR1 + R ) )
= E * (R1 + R – 2R) / ( 2 * ( R1 + ΔR1 + R ) )
= E * (R1 – R) / ( 2 * ( R1 + ΔR1 + R ) )
ΔR1がゼロの時は、
Vo = E * (R1 – R) / ( 2 * ( R1 + R ) )
(3)
R1 が R1+ΔR1 になった時、ブリッジ出力電圧は、
Vo = E * (R1 +ΔR1 – R) / ( 2 * ( R1 +ΔR1 + ΔR1 + R ) )
R1 が R と同じ抵抗値になるように調整すると、
Vo = E * (R +ΔR1 – R) / ( 2 * ( R +ΔR1 + ΔR1 + R ) )
= E *ΔR1 / ( 4 * ( R + ΔR1 ) )
(4)
R1 >>ΔR1 とすると、
Vo ≒ E *ΔR1 / 4R
(5)
0.2%の抵抗増加がR1に生じた時、
ΔR1 = R1 / 500
出力電圧は、
Vo ≒ E *ΔR1 / 4R
= E * R1 / 2000R
= 2 * 100 / (2000 * 100)
= 1 / 1000
= 1 [mV]
問7
(1)
長さがLの物質に電圧をVをかけた時、その内部の電界は、
E = V / L
(2)
電子が電界から受ける力は、電子の電荷を -e とすると、
F = e * E = e * V / L
(3)
運動方程式より、
m * a = F
上記をFに代入すると、
m * a = e * V / L
※問題文では質量を me にしてますが、まどろっこしいので m だけにしてます
加速度は、
a = e * V / ( m * L )
(4)
問題文より、最終的に落ち着く電子の移動速度vdriと、散乱により働く力F2の関係は、
F2 = vdri * m / τ
※問題文では v のみとなってますが、電圧の V と混同するので vdri にしてます
最終的に速度が一定になっていると言うことは F = F2なので、
vdri * m / τ = e * V / L
これを整理すると、
vdri = e * V * τ / ( m * L )
= e * τ / ( m * L ) * V
(5)
物質中の電子密度が n の時、特定のラインを単位時間当たりに通過する電子の数 N は、
N = n * S * vdri
単位時間当たりに通過する電荷の総量が電流であるため、電流 I は、
I = e * N
= e * n * S * vdri
= e * n * S * e * τ/ ( m * L ) * V
= e2 * n * S * τ/ ( m * L ) * V
この問題を間違えてしまったのは、e を掛け忘れたためです。不覚・・・
電力

話になりませんね。
機械

取りたいところは取れたかなという印象。あとは選択問題マジック。
問2
(2)
図3では立ち上がり時間が考慮されているように見えるが、(2)の段階では理想スイッチという前提なので無視できるはず。キルヒホッフの第二法則より、
Vdc = vs + v
なので、vs = Vdc の時は v = 0 で、vs = 0 の時は v = Vdc になる。スイッチがONの時にスイッチにかかる電圧(つまりvs )がゼロで、周期 T のあいだのうち D*T の期間にONにすると書いてあるので、ダイオード電圧 v の平均値は、
V = Vdc * D * T / T
= Vdc * D
(4)
図3を見たところ、瞬時電力(これが損失の模様)を示す波形は三角形。ターンオフの部分を見ると、頂点の高さは Vdc と Idc の積、底辺の長さは T2 になっている。縦軸が電力、横軸が時間であるため、この三角形の面積がエネルギー損失[J]になるはず。なので、
Woff = 1/2 * Vdc * Idc * T2
(5)
1周期辺りの損失[J]は、ターンオン損失とターンオフ損失を足せばいいので、
W = Won + Woff
ずっとオンオフを繰り返した時の損失[W]は、これの時間平均値を出せばいいので、
P = W / T
= ( Won + Woff ) / T
問3
(1)
円のはずなので1周辺りは 2π [rad] で、1秒当たり f 回周回するので、
ωs = 2πf / p [rad/s]
問4
(5)
電池の質量をm、エネルギー密度をWs、放電可能時間をt とすると、
Ws = V * I * t / m
なので、質量は、
m = V * I * t / Ws
= 3.5 * 0.5 * 10 / 175
= 0.1 [kg]
= 100 [g]
問5
(3)
i0(t) = √2 * V1 / Z * sin(ωt – π/2 )、
φ(t) = N1μA / ℓ * i0(t)
= Φm * sin(ωt – π/2 )
と問題文で与えられているので、
Φm = N1μA / ℓ * √2 * V1 / Z
環状鉄心のインダクタンスは、
L = N12μA / ℓ
環状鉄心のインピーダンスは、
Z = ωL
= ωN12μA / ℓ
なので、
Φm = N1μA / ℓ * √2 * V1 / ( ωN12μA / ℓ )
= √2 * V1 / ωN1
なんかこじつけ感が強いですが、そもそも磁束の次元 [ V・s ] に合う選択肢が1つしかない・・・
問6
(1)
輝度の単位はカンデラ毎平方メートルなので、
L = dI / dS
法規

なぜ法規はこんなにも当たるんだ・・・? 謎すぎる・・・
でも改めて問題を見ると、それしかないだろって選択肢もあったりします。
二次試験
記述式なので自己採点が難しいですね。
電力・管理
問1、2、4、6を選択。書いたところが全部当たってないと合格は厳しい印象。
普通に色々と間違えてたので赤字で入れていきます。合格ラインは6割なので、電力・管理は落ちてますね。よくても4割ぐらいの得点でしょう。
問1
(1) 比速度の上限値は問題文で与えられており、
ns ≦ 23000 / (H+30) + 40
右辺を計算すると、
23000 / (162+30) + 40 = 3835 / 24 = 159.79
回転速度と比速度の関係も問題文で与えられており、
ns = N * √P / H5/4
なのでNは、
N = ns * H * H1/4 / √P
= 3835/24 * 162 * √(√162) / √(40 * 103)
= 461. 76
上限値を求める問題なので4桁目以降を切り捨てた上で有効数字3桁で表現すると、N は 461 [min-1] 以下でなければならない。
合ってました。おそらく減点もないかと。ただ、配点は分からない。(1)~(3)で均等に分けてるってことはないと思われる・・・。
(2) ワ・カ・ラ・ナ・イ・ヨ
おそらく 120*f/p の逆算から、461min-1付近で取り得る回転速度は400、450、515min-1で、フランシス水車は比速度180付近で高効率となること、高速で回すほど小型化でコストも低減されることから、461min-1以下を守れる最大値の450がmin-1が正解。
(3) ワ・カ・ラ・ナ・イ・ヨ
(2)で決めた450min-1から 120*f/p で逆算すれば、16極。
問2
(1) 役割は、高電圧・大電流を計器で測定できるレベルまで低下させること。
代表的なもの2つは、計器用変圧器と計器用変流器。
ε = ( 1 – K / Kn ) * 100 [%]
うーん、説明不足感が否めない。少なくとも、リレーや計器を高圧回路から絶縁する旨を書いてないのは減点対象でしょう。式も間違えてて、模範解答では (Kn – K) / K * 100。分母は Kn じゃなくて K だった。
(2) ワ・カ・ラ・ナ・イ・ヨ
模範解答は箇条書きになってますが、正直問題文との対応がよく分からないので書けません(自分が説明できないことは書かない主義です)。気になる方は公表されている模範解答を直接参照してください。
(3) ワ・カ・ラ・ナ・イ・ヨ
サイクル数は5及び3、事故除去指令を受ける箇所の名称は引外しコイル(トリップコイル)、トリップフリーの機能と目的は模範解答を参照。
問4
(1) 面倒なので図は省略します。
単相3線式は、100Vに加えて200Vを供給することができるため、汎用性が増す。200Vを供給することができる一方で、中性線を接地すれば最大対地電圧は100Vに抑えることができるため、安全性についても遜色ない。また、単相2線式と比べて1.5倍の配線で2倍の負荷が置けるため、材料費が節約できる。
まず、省略した図面ですが、模範解答ではトランスが描いてある(一次側は6600V)一方で私は交流電源の記号で考えていたので、これで減点される恐れがあります。ただ、問題文が不親切だと言わせて頂きたい・・・ですが、トランス込みで考えるのがプロの間では普通かも知れず、その辺りも採点対象だと言われたら返せる言葉はありません。
利便性の記述は減点されないと思いますが、安全性の記述で、3線式なら対地電圧が200Vにならない旨を書いてないのは減点される可能性が高いです。というか 1Φ2W100V と 1Φ3W100/200V との比較でしか書いてませんでした。やっぱり問題文不親切じゃないか・・・? というのは負け惜しみか。
(2) 単相2線式の負荷を 2P、単相3線式の各負荷を P 、配線抵抗を rw とすると、単相2線式の場合の電流 I2 及び 電圧降下 Vdrop2 は、
I2 = 2P / (V*cosΘ) = 2P / (100*cosΘ)
Vdrop2 = 2 * I2 * rw = 2 * 2P / (100*cosΘ) * rw = 4P*rw / (100*cosΘ)
続いて、単相3線式の電流 I3 、
I3 = P / (V*cosΘ) = P / (100*cosΘ)
上下で負荷が同じ場合は中性線に電流が流れないため、電圧降下 Vdrop3 は、
Vdrop3 = 2 * I3 * rw = 2 * P / (100*cosΘ) * rw = 2P*rw / (100*cosΘ)
このように、単相3線式では単相2線式と比較して電圧降下が小さい。
結論から言うと、単相3線式の電圧降下は単相2線式の1/4になるのが正解なので間違ってます。2倍ズレた原因は、模範解答では3線式での電圧降下が1線分のみとなっているためです(つまり Vdrop3 = I3 * rw とするのが正解)。私が 2 * I3 * rw としたのは、100V負荷の2直列で考えて赤線と黒線の2線で電圧降下があるとしたためです(負荷が2つになる分の補正として2線式の負荷を2Pにした)。しかしどうやら、3線式での計算は赤線(あるいは黒線)と白線の100V回路のみで考えれば良かったらしく、模範解答ではその補正として電流を2倍にしています。3線式の回路全体で考えたら何度やっても上のようになるので煮え切らない・・・ですが、公式の解答がそうなっている以上、実際に1/4になるのでしょう。
(3) 中性線の欠相により生じる障害は、負荷が不均衡である場合は電圧に偏りが生じ、100V定格負荷にそれ以上の電圧が印加されることとなるため、負荷の破壊、及びそれを基にした波及事故につながる。原因は、過電流による断線や小動物による被害など。対策は、過電流を検知し遮断するシステムを導入する、小動物の侵入を防ぐなど。
障害の記述として、片方の過電圧にしか触れずもう片方への印加電圧低下に触れなかったのは減点されるかも? そこがセーフでも小動物がどうとかは採点者も鼻で笑うでしょうね。模範解答にある、導体の温度変化に伴う膨張・収縮や振動等による経年劣化は確実に起こるので、そっちを書くのが自然でしょう。
問6
(1) P1 の負荷で必要とされる皮相電力を S1 とすると、
S1 = P1 / cosΘ1 = 6000 / 0.8 = 7500 kVA
ベクトル表示すると、
S1 = P1 – j S1*sinΘ1 = 6000 + j 7500 * √(1-0.62) = 6000 – j 4500 kVA
同様にS2は、
S2 = P2 / cosΘ2 = 4500 / 0.6 = 7500 kVA
ベクトル表示すると、
S2 = P2 – j S2*sinΘ2 = 4500 – j 6000 * √(1-0.62) = 4500 – j 6000 kVA
したがって、必要とされる皮相電力の合計は、
Stotal = S1 + S2 -jQ1 -jQ2
= 10500 – j 10500 + j 2000 + jQ2
= 10500 – j ( 8500 – Q2 )
その絶対値が変圧器容量である 12000 kVA となるQ2を求めると、
√(105002 + (8500-Q2)2) = 12000
(8500-Q2)2 = 120002 – 105002
Q2の下限値のみを求めれば良いため、右辺の平方根の負は考えない。
8500 – Q2 = √(120002 – 105002)
Q2 = 8500 – 100√3375
= 2691
下限値を求める問題なので4桁目以降を切り上げた上で有効数字3桁で表現すると、Q2 は 2.70 * 103 [kvar] 以上必要である。
また、この時の総合力率cosΘsは、
cosΘs = 10500 / √(105002 + (8500-(8500-100√3375))2)
= 10500 / √(105002 + (100√3375)2)
= 105 / √(1052 + 3375)
= 0.875
ほぼ模範解答通り。減点もないはず。
(2) 面倒なので図は省略しますが、P2は右に4目盛半の矢印になります(多分、既に引いてあるQ1の矢印の先端をスタートにする)。その皮相電力を示す斜めの矢印はQ1の先端基準で右に4目盛半、下に6目盛の位置に引っ張ります。その角度がΘ2で、皮相電力の矢印の先から真上に2.7目盛の方向に書くのがQ2です。このQ2の矢印の先端が、変圧器容量を示す点線のカーブに重なるはずです。
Q1の先端を起点に描くで合ってましたね。こればかりは問題文が不親切と言っても良いんじゃなかろうか。何の説明もなく「PTの点線があることから全てを察しろ」みたいになってる。
(3) 総合力率を0.95とするための Q2 を求めると、
10500 / √(105002 + (8500-Q2)2) = 0.95
√(105002 + (8500-Q2)2) = 10500 / 0.95
(105002 + (8500-Q2)2 = (10500 / 0.95 )2
(8500-Q2)2 = (10500 / 0.95 )2 – 105002
総合力率は遅れを前提としているため、右辺の平方根の負は考えない。
8500-Q2 = √( (10500 / 0.95 )2 – 105002 )
8500-Q2 = 10500√( (1/0.95 )2 – 1 )
8500-Q2 = 10500√( (1-0.952)/0.952 )
8500-Q2 = 10500/0.95 * √(1-0.952)
Q2 = 8500 – 10500/0.95 * √(1-0.952)
Q2 = 5049
下限値を求める問題なので4桁目以降を切り上げた上で有効数字3桁で表現すると、Q2 は 5.05 * 103 [kvar] 以上必要である。
解き方は違えど、論理に間違いはないので減点もないはず。まともに解けたのは問6だけだったね・・・。
機械・制御
問3、4を選択。問3は個々の問題が独立してる一方、問4は最初で外すとほぼ全滅するのが怖いところ。
問3でまさかの位相差プラスマイナスのミス。問4は(1)と(3)でマイナスがない(本番ならブロック図ちゃんと描くから間違えないはず・・・!)のがどう減点されるかですが、トータル6割には乗ると思われます。ただ、合格ラインには「受験者の平均点以上」もアンドとしてあり、その平均点が公表されていないので分かりません。電力・管理が落ちてるので一緒ですが。
問3
(1) 図2より、位相が ω0t の時、Nu = 1、Nv = 1である。Nu や Nv が 1 の時に各相の上アームがオンであると定義されているため、Q1とQ3がオン状態にある。
大正解!
(2) Q4のコレクタ・エミッタ間電圧を v4 とすると、キルヒホッフの第二法則より、Ed/2 + vvo = v4 であるため、
vvo = v4 – Ed/2
Nv = 0 の時はQ3がオフ、Q4がオンであり、Ed は全てQ3に印加されるため、v4 = 0
Nv = 1 の時はQ3がオフ、Q4がオンであり、Ed は全てQ4に印加されるため、v4 = Ed
したがって、vvo の波形は以下のようになる。※面倒なので波形は書きません
・Nv = 0 の時は、vvo = – Ed/2
・Nv = 1 の時は、vvo = Ed/2
また、
vuv = vuo – vvo
であるため、vvo の波形は以下のようになる。※面倒なので波形は書きません
・Nu = 1 かつ Nv = 0 の時は、vuv = Ed/2
・Nu = 1 かつ Nv = 1 の時は、vuv = 0
・Nu = 0 かつ Nv = 1 の時は、vuv = – Ed/2
・Nu = 0 かつ Nv = 0 の時は、vuv = 0
多分ここも、解答用紙にある図に線を描くだけでいいはずなので、外さない。
(3)
この運転方法において、i0 > 0 で vuv がゼロになった直後は、Q1とQ3がオン、Q2とQ4がオフの状態である。したがって電流は点vを通過後は上アームに向かう。Q3はオンであるが、図記号からIGBTであるため、経路はD3のみである。その後、Rに至るまでの経路は、Q1を通るか、E及びD2を通るかであるが、Q2がオフであるためにD2はアノードの方が電位が低くなっており、導通しない。したがって、電流はQ1を通ってRに至る。したがって、指示通りに電流経路を示すと、
L – D3 – Q1 – R – L
となる。
続いて、i0 < 0 で vuv がゼロになった直後は、Q2とQ4がオン、Q1とQ3がオフの状態である。まず、i0<0であるため、Lの次はRを通る、点uを通過後はD1あるいはQ2を通ることになるが、Q1がオフであるためにD1はアノードの方が電位が低くなっており、導通しない。したがって、電流はQ2を通る。その後も、Q1とQ3が共にオフであるためEを経由して上アームに至ることはなく、電流はD4へと向かう。D1と同様にD3も導通しないため、点v通過後はLに戻る。したがって電流経路は、
L – R – Q2 – D4 – L
となる。
こちらもビンゴ! ただ、頑張ってロジックを書いたのに模範解答がマジで答えしか載ってないのは不服・・・。
(4) 基本は成分は n = 1 の項であるため、その瞬時値は、
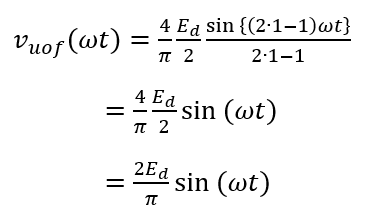
となる。
なぜここも模範解答は答えしか書いてないんだ・・・。
(5) 図2より、vvo は vuo の 2π/3 遅れである。vuv = vuo – vvo であるため、その基本波成分は、
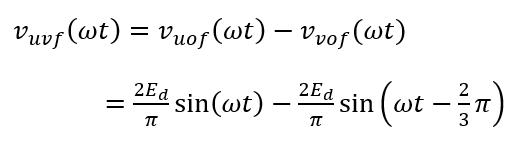
となる。このベクトル図は下図のようになり、vuof 及び vvof の最大値が 2Ed/π であることを基にvuv の最大値を求めると、
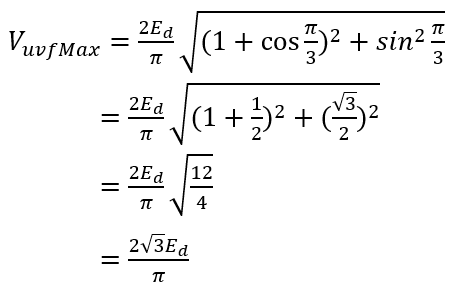
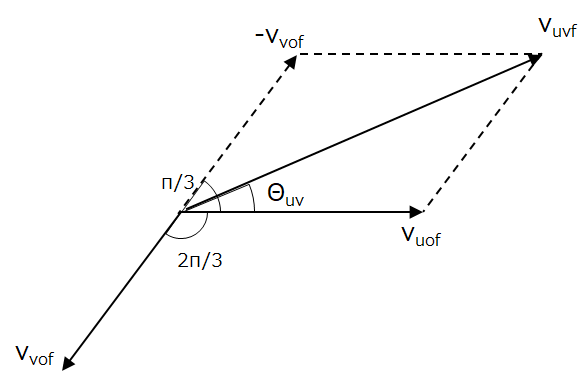
また、vuv の位相をΘuvとすると、
Θuv = cos-1( (1 + 1/2 ) / √(12/4) )
= cos-1( (3/2 ) / √3 )
= cos-1(√3/2)
ベクトル図より、0 < Θuv < π/2 であるため、
Θuv = π/6
したがって、vuv の瞬時値は以下のようになる。
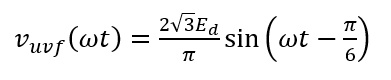
ベクトル図まで描いておきながらプラスマイナス間違えるとかアホ。ベクトル図があるので1~2点しか減点されないと思いますが。
また、この実効値は、
2√3 * Ed / π * 1/√2 = √6 / π * Ed = 0.780 * Ed
となるため、Ed の0.780倍となる。
模範解答では「√6 / π 倍」となってますが、それ計算して0.780を出すぐらいは問題ないはず。
問4
(1) R(s) = 0、C(s) = K(>0) の時、D(s) に対する E(s) は、
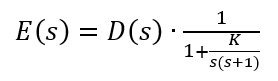
となる。t ≧ 0 において d(t) = 2t なので、
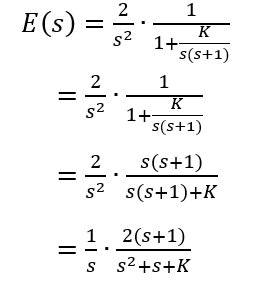
定常速度偏差 ev は、
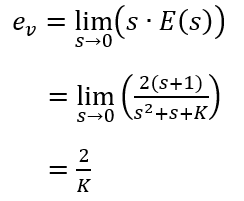
図を描くのサボったために最初の式の段階でマイナスを入るはずが抜けてそのまま最後まで行ってしまいました。ちゃんと図を描けば見落とさないはず・・・ですがもし見落としたら大きな減点は免れないでしょう。
(2) E(s) = 1/s * 2(s+1)/(s2+s+K) より、
・2ζωn= 1・・・①
・ωn2 = K ・・・②
K > 0 であるため ωn は正の実数であり、
ωn = √K
これを①に代入すると、
2ζ√K= 1
ζ を 0.8 にするための K は、
K = ( 1 / (2*0.8) )2
= 0.391
(1)とは独立した計算になるので、減点されないはず。
(3) R(s) = 0、C(s) = A(s+1)/(0.1s+1) の時、D(s) に対する E(s) は、
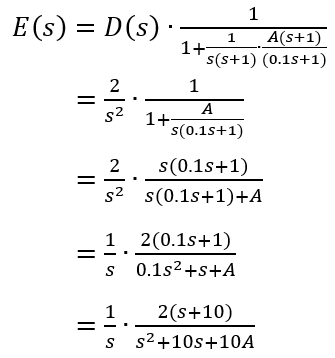
標準速度偏差 ev は、
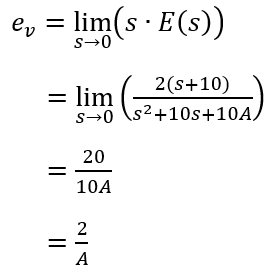
ここもマイナスがないのは(1)と同じ。マジでこれやったらいくら減点されるのだろうか。
(4) E(s) = 1/s * 2(s+10)/(s2+10s+10A) より、
・2ζωn= 10・・・①
・ωn2 = 10A・・・②
A > 0 であるため ωn は正の実数であり、
ωn = √(10A)
これを①に代入すると、
2ζ * √(10A) = 10
ζ を 0.8 にするための A を求めると、
√(10A) = 10 / (2*0.8)
√A = √10 / 1.6
A = 10 / 1.62
A = 3.91
ここも(3)とは独立した計算なので、減点されないはず。
(5)
上記(2)の場合、ωn = √K = 1 / (2*0.8) = 0.625
上記(4)の場合、ωn = √(10A) = 10 / (2*0.8) = 6.25
従って、(2)の場合に比べて(4)の場合は応答が10.0倍速い。
ここもきっと減点はない!
(6)
上記(2)の場合、ev = 2 / K = 2 / (1/1.62) = 5.12
上記(4)の場合、ev = 2 / A = 2 / (10/1.62) = 0.512
従って、(2)の場合に比べて(4)の場合は定常速度偏差が 0.100 倍になる。
最終的な答えは合ってますが、5.12 と 0.512 にマイナスがないのがどう影響するかは分かりません。ただ、ロジックそのものに欠陥はないので、(1)や(3)ほどの減点にはならないはず。
という訳で、機械・制御は何とか合格しそうですが電力・管理はダメですね。なお、この年の合格者は例年の2倍ほどの701人。それで落ちたとかダメじゃん・・・。
ちなみに、1つ前の年から2年連続で「例年の2倍の合格者」になってるようです。おそらく後継者不足対策と思われますが・・・人を増やす方法として試験問題が低難易度化されたなら、ちょっと業界に影が差してるんじゃないかと思いたくなってしまいますね。